Los siguientes problemas están ordenados por nivel de complejidad.
EXPRESIONES
1. Cinco veces un número aumentado a la mitad de otro número.
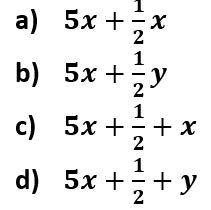
2. La familia Gómez quiere comprar un paquete de excursión al volcán Iztaccíhuatl que cuesta $120 para los adultos. El costo por niño es $30 menos que la mitad del costo para adultos. ¿Cuál expresión representa el costo para cuatro niños?
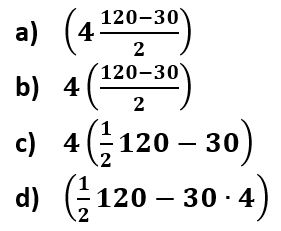
ECUACIONES
3. El doble de un número, reducido por 15, es igual a cuatro veces el mismo número.
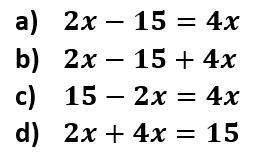
4. Carla gastó 1/3 de su salario mensual en un mueble para su sala. Después gastó $80 para surtir su despensa. Hasta ese momento ya había gastado la mitad de todo su salario. ¿Cuál ecuación representa esta información?
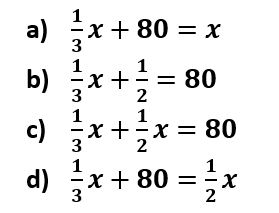
5. Laura hace cortes de pelo en sus ratos libres. Por cada corte de pelo cobra $25 dólares y recibió $115 de propina. ¿Cuál expresión muestra cuántos cortes de pelo hizo esta semana si en total ganó $410?
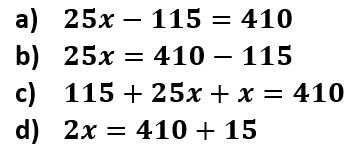
6. Un lazo de 36ft de largo es cortado en tres pedazos. El segundo pedazo es 4gt mas largo que el primero y la ultima pieza es 3 veces mas largo que la segunda. Si x representa la longitud de la primera pieza, entonces: ¿Cuál ecuación determina la longitud de la primera pieza?
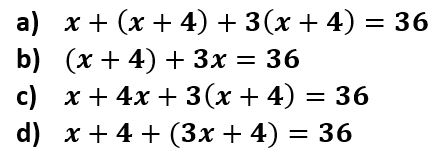
DESIGUALDADES
7. La suma de un número y 12 es menor o igual a 7 por el número más ocho. ¿Qué desigualdad representa esta situación?
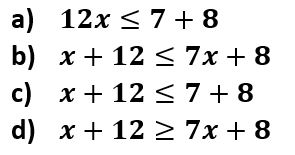
8. Luisa quiere comprar pulseras para sus amigas y solo tiene $40 dólares para gastar. Si cada pulsera cuesta $4.20, ¿Qué desigualdad muestra el número de pulseras que puede comprar?
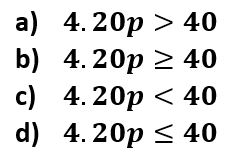
ECUACIONES LINEALES
9. Alicia está entrenando para un maratón y todos los días corre la misma distancia, si para el quinto día lleva recorridas 29 millas, ¿cuál ecuación muestra cuántas millas va a registrar para el noveno día?
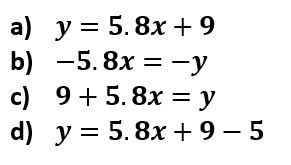
ECUACIONES SIMULTANEAS
10. Gabriela es tesorera de la cooperativa Almanza, que elabora tapetes sólo de dos tamaños. El precio de los tapetes chicos es de $250.00 y de los grandes de $450.00. Al hacer su relación de ventas de ayer, le dijeron que en total habían vendido 12 piezas de tapetes de los dos tamaños y reunido $4 000. ¿Cuántos tapetes chicos y cuántos grandes vendió?
RESPUESTAS
- b, 2. c, 3. a, 4. d, 5. b, 6. a, 7. b, 8. d, 9. b, 10. 7 chicos y 5 grandes


Maestra con el ejercicio 10. se me fundio el cerebro
Sí, la 9 y la 10 son las más difíciles y más aun porque no es de opción multiple.
Aquí te pongo los pasos, también lo encuentras al final del video.
Primero hay que clasificar precio de las alfombras y cantidades de alfombras y representarlo en ecuación
a) $250x + $450y = $4000 precios
b) x + y = 12 cantidad de alfombras vendidas
Puedes igualar multiplicando la ecuación b por -250 para eliminar las x
a) 250x + 450y = 4000
b) -250x – 250y=-3000 Ahora restas y sumas según corresponda y queda
0 + 200y = 1000 Despejas la y dividiendo
y = 1000/200
y = 5
Para obtener el valor de x, sustituye el valor de «y» en cualquiera de las ecuaciones
x + 5 = 12 Despejas
x = 12 – 5
x = 7
En el video use el método de igualación que también da el mismo resultado.
¡Saludos!
como resuelvo este problema Entre Iván, Ernesto y Karla juntaron $13500, Iván tiene el doble de lo que juntaron Ernesto y Karla; además, Ernesto tiene la mitad de lo que tiene Karla ¿cuándo es lo que tiene Karla? gracias
Primero debes identificar quien representa a la «x» y va a ser Karla, Ernesto tiene la mitad de Karla por tanto es 1/2x (un medio de x) y por último Iván tiene el doble de lo que Karla y Ernesto juntaron por tanto multiplicas esos valores por 2 y te queda 2(x +.5x)
x = Karla
.5x = Ernesto, la mitad que es 1/2 o .5
2(x +.5x) Iván
Representando la ecuación tenemos:
x + .5x + 2(x + .5x) = 13500 despejas paréntesis
x +.5x +2x + x = 13500 sumas las x
4.5x = 13500 Despejas el 4.5 dividiendo
x = 13500/4.5
x = 3000
cada semana jose alfredo retira $200.00 del banco duarante 4 semanas como podría representar numéricamente esta situación? ¿cual es la representación de la adición y suma?
como represento la multiplicacion y el producto? y cuanto dinero retiro en total?
En este enlace se explica como se representan la adición, el producto, etc. (producto quiere decir multiplicación. En álgebra se representa con paréntesis ( ), asterisco * o un punto media altura ·
También indica multiplicación si tienes un número y una letra juntas como 2x, 5y,8xy, etc.
Para el ejercicio, Alfredo retira $200 durante 4 semanas solo pones 4(200)
Ahora si te dijeran que Alfredo retira $200 durante cierto número de semanas (y no te indican cuantas, esa es tu incógnita o letra) Y lo pondrías así 200x – donde x representa el número de semanas.
También te pueden decir. Alfredo retira cierta cantidad de dinero durante 4 semanas y en ese caso puedes poner 4x (no necesariamente tienes que usar la x, puedes usar cualquier letra pero en álgebra es común que se use la «x» para representar un valor desconocido.
Hola
Hola Isaac.
Como resolver este problema. De 1990 a 1994 el costo básico de una habitación privada en el Hospital Metropolitano aumento de $600 a $680. Si hay c cuartos privados en el hospital. Escribe una expresión algebraica que indique cuando dinero más recibió el hospital diariamente por todos los cuartos en 1994 en comparación con lo que recibió en 1990
Para representar el dinero recibido en 1994 multiplica los 365 días del año por el número de cuartos y el costo por cuarto : 365(680c)
Para 1990 sería 365(600c)
Excelente pagina, lastima la cantidad exagerada de anuncios, no me permitieron siquiera poder leer algunos problemas, porque aparecen sobre ellos y no hay forma de cerrarlos.
Gracias por tu comentario Jenn, voy a revisar si podemos cambiar la configuración de las publicaciones. Saludos!
Luis tiene 12 años y Pedro 17. ¿Hace cuantos años, la edad de Pedro era el doble de la de Luis?
Espero la explicación escrita quede clara:
Primero escribe las edades representadas en el presente y el pasado
PRESENTE PADADO
Luis 12 12-t
Pedro 17 17-t
(t, representa el tiempo en años y restamos porque es en el pasado)
Escribimos la ecuación:
17-t = 2(12-t) /Aumentamos el 2 porque la edad de Pedro era el doble de la de Luis.
Para resolver, primero multiplica el 2 por 12 y el 2 por t, te queda:
17-t = 24-2t Despejas las t y los números, pasandolas al otro lado del simbolo de igualdad con el signo contrario
2t-t = 24-17 Resuleves las restas
t= 7 (Hace 7 años Pedro tenia el doble de edad de Luis) Puedes comprobarlo restando 7 a las edades actuales.