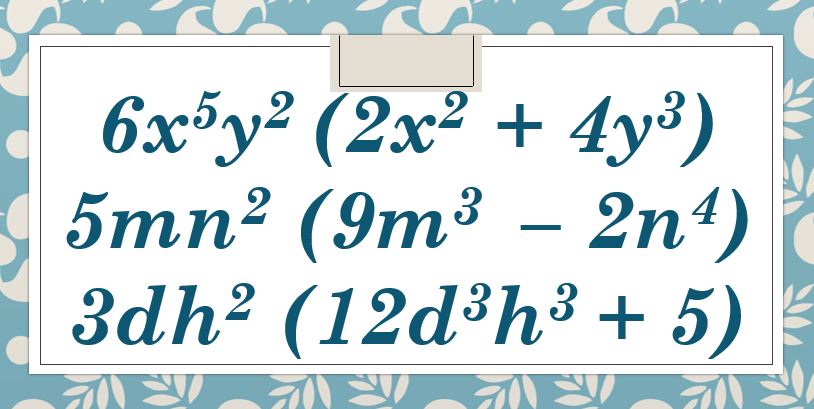
Máximo común factor
Una vez que hemos aprendido a encontrar en común factor usando números, vamos a practicar un poco como obtener el común factor usando literales (letras).
Para encontrar la literal (letra) común, hay que observar cual es común a cada uno de los términos y escoger la que tenga el exponente mas chico. Por ejemplo, si tenemos x4 + x2, de estos dos términos el que tiene el exponente más chico es el x2, esa va a ser la literal común.
Si un término tiene más de una literal con exponentes diferentes se aplica el mismo procedimiento con cada literal.
Ejemplo x6y3 + x2 + y7 – x3y3, en este caso la literal “x” con el exponente más chico es x2 y la literal “y” con el exponente más chico es y3, al final los literales comunes son x2y3.
En seguida se presentan tres ejercicios para identificar las literales comunes: (No hay que sumar o restar, solo buscar las literales comunes)
- m6n3, m8n2, m5n7, m3n6
- x2y5z9, x5y12z11, x3y3z8
- a15b3, a3b, a5b6, a2b7
Respuestas, literal común.
- m3n2
- x2y3z8
- a2b
El siguiente paso es aprender a buscar el “máximo común factor” y para esto se combinan el común factor y las literales comunes, en otras palabras, vamos a combinar números y letras.
Ejemplo I
6x2 + 15x
PASO I
Identifica el común factor (2)(3) = 6 y (3)(5) = 15, el común factor es 3
PASO II
Identifica la literal común, ósea la letra que tiene el exponente más chico y es la “x”
PASO III
Escribe los factores comunes (el 3 y la “x”) fuera del paréntesis y los restantes (los números que sobran del PASO I, que son el 2 y 5) dentro del paréntesis expresando multiplicación de términos 3x (2x + 5)
IMPORTANTE: Para determinar que literal (letra) va dentro del paréntesis, hay que restar el exponente de la literal con la literal común
x2 – 1 = 1
También se pude obtener dividiendo, como se explica mas abajo.
PASO IV
Para comprobar se multiplica y se debe obtener las expresión inicial.
3x (2x + 5)
6x2 + 15x
EJEMPLO II
45m5n3 – 10 m2n
PASO I
Identificar el común factor, (3)(3)(5) = 45 y (2)(5) = 10. El común factor es 5
PASO II Identificar la literal común (letras que tienen el exponente más chico) m2n
PASO III
Escribir el común factor y la literal común fuera del paréntesis. Dentro del paréntesis se escriben los términos restantes respetando los signos de multiplicación.
5m2n (9m3n2 – 2)
IMPORTANTE: para determinar que exponente van a llevar las literales dentro del paréntesis, solo se restan los exponentes de la expresión original con los exponentes de la literal común que no es otra cosa que la división.
m5 – 2 n3 – 1
m3n2.
Solo un repaso, se resta porque si recuerdas, en la multiplicación de términos, al multiplicar se suman sus exponentes y factorizar es lo contrario a multiplicar, ósea dividir.
También puedes dividir la expresión original entre el máximo común factor y nos quedaría así.
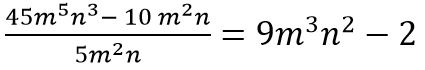
La respuesta anterior es la que va dentro del paréntesis y el máximo común divisor fuera 5m2n (9m3n2 – 2)
Pasos para la división:
(Hay que dividir la expresión que queremos factorizar entre el máximo común divisor 45m5n3 ÷ 5m2n)
- Se divide el signo usando la misma regla de multiplicación de signos (+ • + = +)
- Se dividen los coeficientes -números- (45 ÷ 5 = 9)
- Se dividen las literales (letra) (OJO) al dividir incognitas se restan sus exponentes m5-2 =3 = m3 y n3-1 =2 = n2
- Por último para dividir (– 10 m2n ÷ 5m2n) se repiten los mismos pasos. Solo al final, al dividir las literales, como tienen el mismo exponente, se eliminan y no se escribe ninguna literal, solo el –2.
Ejemplo II
4a2b3 – 6a3b2 + 8a4b
PASO I
Obtener el común factor (2)(2) = 4, (2)(3) = 6, (2)(4)= 8. El común factor es 2
PASO II
Identificar la literal común y es a2b
PASO III
Escribe el común factor y la literal común fuera del paréntesis y el resto dentro del paréntesis 2a2b (2b2 – 3ab + 4a2) Si se te dificulta obtener los términos que van dentro del paréntesis, también puedes dividir la expresión original entre el máximo común factor o simplemente resta los exponentes del ejercicio original con la literal común. El otro método es dividir.
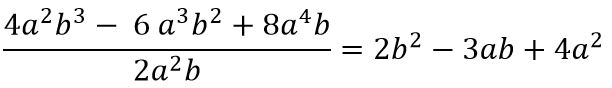
PASO IV
Comprueba tu respuesta multiplicando.
a2b (2ab2 – 3ab + 4a2b)
EJERCICIOS DE PRACTICA
- 42x2 + 30x
- 15m2 + 6m
- 40y2 + 35y
- 10x2 + 40x
- 18z2 + 4z
- 12x7y2 + 24x5y5
- 45m4n2 – 10mn6
- 36d4h5 + 15dh2
- 8m6n2p – 36mn3p5
- 44x5y7z + 11x2y3z4
RESPUESTAS
- 6x (7x+5)
- 3m (5m +2)
- 5y (8y + 7)
- 5x (2x + 8)
- 2z (9z + 2)
- 6x5y2 (2x2 + 4y3)
- 5mn2 (9m3 – 2n4)
- 3dh2 (12d3h3 + 5)
- 4mn2p (2m5 – 9np4)
- 11x2y3z (4x3y4 + z3)
