Cómo obtener la parabola de un trinomio
Los trinomios de segundo grado o trinomio cuadrado son aquellos que tienen tres términos. El primero va a tener una literal al cuadrado, el segundo su literal estará a la potencia uno y el último término no tendrá literal. Por ejemplo:
2x2 + 6 x – 4.
I Fórmula cuadrática para obtener las raíces
Si tenemos un trinomio cuadrado se pueden buscar sus factores, quiere decir encontrar los términos que multiplicados entre si nos dan el trinomio. Ese es un método para obtener los valores de “x” que también se pueden obtener aplicando la fórmula cuadrática. A esas “x” las vamos a llamar raíces, que no es otra cosa que los puntos por los que atraviesa una parábola en la coordenada de “x”. Es posible que algunos trinomios cuadrados no tengan raíces, ósea, que no toquen la coordenada de “x”.
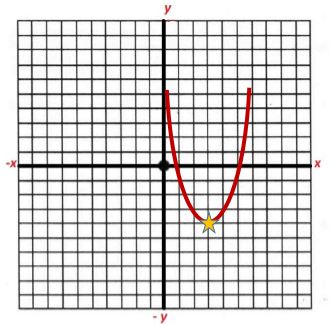
La siguiente ilustración muestra un ejemplo, las raíces siempre se van a encontrar en el punto en que cruzan la parábola y la coordenada de “x”.
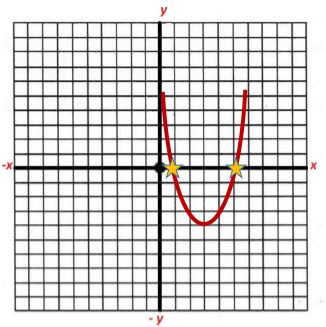
Para encontrar las raíces veamos el siguiente ejemplo aplicando la fórmula cuadrática en el siguiente trinomio cuadrado
x2 – 6x + 5
Paso I
Igualar el trinomio a cero para convertirlo en ecuación x2 – 6x + 5 = 0
Paso II
Asignar los valores “a”, “b”, “c”. Si aún no sabes asignarlos revisa este enlace.
- El valor de «a» siempre va a ser el coeficiente del término que esta elevado al cuadrado.
- El valor de «b» va a ser el coeficiente del término cuya potencia es 1.
- El valor de «c» va a ser el coeficiente que no tiene ninguna incognita.
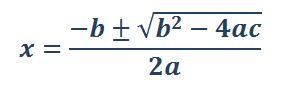
Paso III
Sustituir los valores de a, b, c en la fórmula.
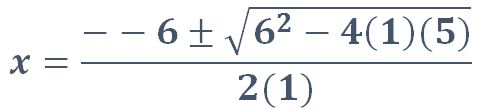
Paso IV
Resolver para encontrar los dos valores de “x”, algunas veces estos pueden ser negativos o en otras posiblemente no se puedan obtener. Valores para «x» x = 1, x = 5. Para aprender a aplicar la fórmula cuadrática se puede visitar este enlace fórmula cuadrática.
Paso V
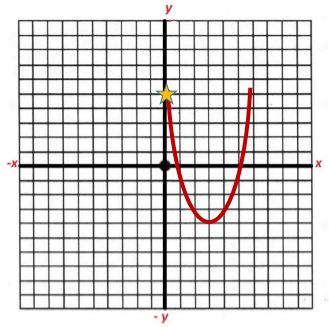
Representar las coordenadas asignando el valor de cero a las “y” (1, 0), (5, 0) que son las raíces de la primera imagen.
Para probar que los valores de “y” son cero pueden sustituir los valores de “x” en el trinomio cuadrado.
Sustituyendo x = 1
y = x2 – 6x + 5
y = (1)2 – 6(1) + 5
y = 1 – 6 + 5
y = 0
Sustituyendo x = 5
y = x2 – 6x + 5
y = (5)2 – 6(5) + 5
y = 25 – 30 + 5
y = 0
Las raíces están representadas por las estrellas amarillas.

II Intercepto en “y”
Con el trinomio cuadrado también podemos encontrar el intercepto en “y”, este es un poco mas sencillo. Si ya sabes sustituir valores en la ecuación ya que solo consiste en darle a la “x” el valor de cero. Veamos
y = (0)2 – 6(0) + 5
y = 5
Las coordenadas del intercepto en “y” van a ser (0, 5). Después de practicar un poco te vas a dar cuenta de que no se necesita llevar a cabo la ecuación, ya que el valor de “y” siempre va a ser “c” ósea el tercer término del binomio cuadrado.
III Vértice o punto de cambio
El vértice indica el punto en el que la parábola cambia de dirección. Para obtenerlo se usa una parte de la fórmula cuadrática y seguir los siguientes pasos.
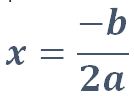
PASO I
Sustituir los valores de “a” y “b” en el binomio x2 – 6x + 5 = 0 y resolvemos
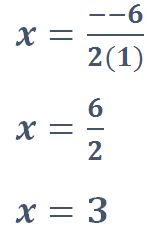
PASO II
Sustituimos el valor de “x = 3” para encontrar el valor de “y”
y = x2 – 6x + 5
y = (3)2 – 6(3) + 5
y = 9 – 18 + 5
y = – 4
El vértice queda en la coordenada de (3, – 4)
IV Funciones
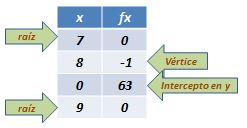
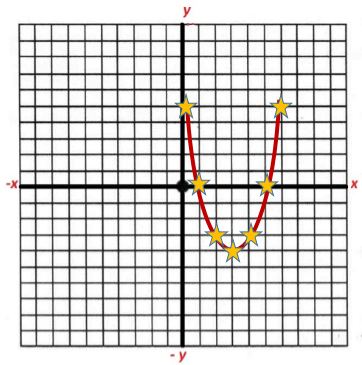
Lo siguiente es escribir los valores de las coordenadas que hemos obtenido y representar la función en una tabla.
Para encontrar otras coordenadas, solo hay que asignar valores a la “x”, pueden ser incluso fracciones y cada una de esas coordenadas van a representar la parábola.
Sustituyendo x = 2
y = x2 – 6x + 5
y = (2)2 – 6(2) + 5
y = 4 – 12 + 5
y = – 3
coordenada (2, – 3)
Sustituyendo x = 4
y = x2 – 6x + 5
y = (4)2 – 6(4) + 5
y = 16 – 24 + 5
y = – 3
coordenada (4, – 3)
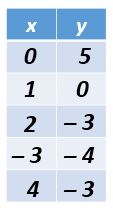
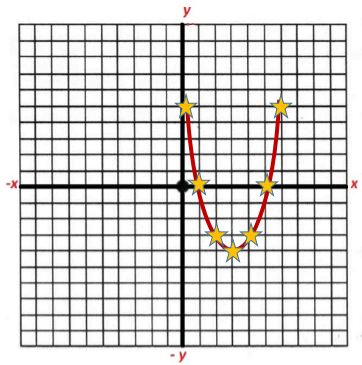
V Graficar las funciones
Una vez que tienes identificas la función, solo queda representar cada una de las coordenadas en el plano cartesiano para representar la parábola.
EJERCICIOS DE PRÁCTICA
1. 2x² – x – 6
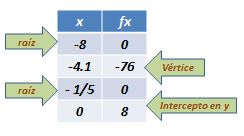
2. 5x² + 8 + 41x
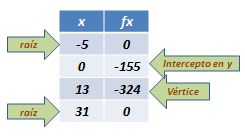
3. x² – 26x – 155
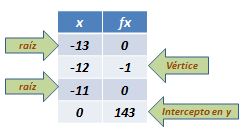
4. 24x + x² + 143
5. 63 – 16x + x²
Deben obtener las raíces, intecepto, vertice; posteriormente graficarlo y representar la función.
RESPUESTAS
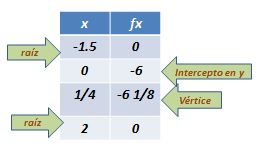
1. 

2. 

3. 

4. 

5.