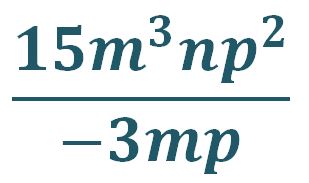
División en algebra
Al dividir en algebra se siguen los mismos pasos que en la multiplicación pero de manera invertida, ósea, haciendo lo contrario. Los pasos para la división son lo siguientes:
- Dividir el signo aplicando la misma regla de la multiplicación
- Dividir los coeficientes o números
- Dividir la incógnita o letra, al hacerlo se restan los exponentes (número pequeños de la derecha y si no hay exponente, este siempre va a ser 1).
EJEMPLO I
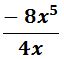
PASO I
Dividir el signo, aplicando la misma regla de la multiplicación.
– / + = –
PASO II
Dividir los números
8 ÷ 4 = 2
PASO III
Dividir incognita o letra restando exponentes (si una incógnita o letra no tiene exponente, este va a ser uno)
x5 ÷ x = x4
La respuesta es – 2x4
EJEMPLO II
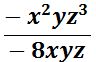
Recuerda que si hay varias letras sin número, este va a ser siempre 1 y cuando dos incógnitas (letras) tengas el mismo exponente, la letra se elimina.
PASO I
Dividir los signos
– / – = +
PASO II
Se dividen los coeficientes (números)
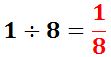
TIP: Siempre que tengas una fracción para dividir queda la misma respuesta, por ejemplo:
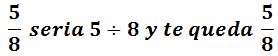
PASO III
Se dividen las incógnitas (letras) restando exponentes, si hay más de una incógnita hay que resolver las semejantes, una por una.
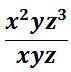
x2 ÷ x = x
y ÷ y = / Se elimina porque 1 – 1 = 0
z3 ÷ z = z2
La respuesta sería:
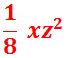
(Ten presente que si el signo es positivo no se escribe)
EJEMPLO III
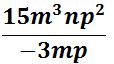
PASO I
Dividir signos
+ / – = –
PASO II
Dividir coeficientes (números)
15 ÷ 3 = 5
PASO III
Dividir incógnitas (letra) restando exponente, (OJO, si solo hay una incógnita, solo se pasa a la respuesta)
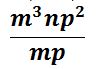
m3 ÷ m = m2
n ÷ 0 = n
p2 ÷ p = p
La respuesta: -5m2np
Regla para exponentes:
Al restar los exponentes toma en cuenta la regla de signos para suma y resta, puedes tener los siguientes casos:
- x5 ÷ x3 = al restar exponentes seria 5 – 3 = 2
- x5 ÷ x -3 = si el segundo exponente es negativo tenemos 5 – -3 = 8
- x -5 ÷ x –3 = si ambos exponentes son negativos tenemos -5 – -3 = -2
- x -5 ÷ x3 = si el primero es negativo tenemos -5 -3 = -8
EJERCICIOS DE PRÁCTICA
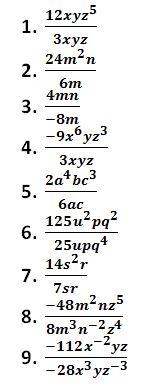
RESPUESTAS
- 4z4
2. 4mn
3. – ½ n
4. – 3x5z2
5. 1/3 a3bc2
6. 5uq-2
7. 2s
8. 6m-1n3z
9. 4x -5z4
