Desigualdades
Las desigualdades nos sirven para indicar cuando una cantidad puede ser igual, más grande o más chica que otra. Para entender y aplicar las desigualdades hay que familiarizarse con los siguientes símbolos <, >, ≤, ≥, =. Veamos un ejemplo de cada uno.
2 < 3 (dos es menor que tres)
5 > 2 (cinco es mayor que dos)
x ≤ 8 («x» es igual o menor a 8)
x ≥ 8 («x» es igual o mayor a 8)
3 = 3 (tres es igual a tres)
Para los siguientes símbolos vamos a usar una “variable” o letra “x” para representar un número desconocido que puede ser representado con la desigualdad.
x ≥ 3 (el número representado por “x” debe ser igual o mayor a tres). Por tanto, el valor de «x» puede ser 3, 4 o mayor.
x ≤ 3 (el número representado por «x» debe ser igual o menor a tres). Por tanto, el valor de «x» puede ser 3, 2, 1, 0, -1 o menor.
Estas desigualdades se pueden representar en la recta numérica, la cual incluye números negativos y positivos. Con respecto a los números negativos hay que verlos un poco a la inversa, por ejemplo -9 es menor a -2, contrario a lo que pasa con los números positivos. Veamos la recta numérica para entender este concepto, vas a poder ver que cualquier número que quede a la izquierda de otro va a ser menor.
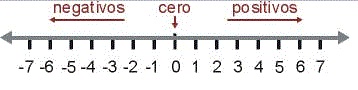
En el lado de los números positivos 3 > 2 (tres es mayor que dos) y como puedes ver el dos esta al lado izquierdo del tres. De igual manera podemos decir que -2 > -3 (negativo dos es mayor a negativo tres) y en este caso el -3 esta a la izquierda del -2. Parece contradictorio, verdad, si tienes dificultad para entenderlo, solo recuerda que el número que queda a la izquierda siempe va a ser menor. También considera que mientras mas grande sea un número negativo, su valor es menor.
Ahora vamos a representar las desigualdades en la recta numérica.
MÉTODO I
La forma más sencilla para representar una desigualdad en la recta numérica es simplemente marcar los posibles valores de la «x». Por ejemplo x < 5 indica que el valor de la «x» es menor a 5 por tanto la x = 4, 3, 2, 1, 0, -1, etc., en la recta numérica tenemos:
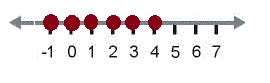
Esa grafica indica que en la desigualdad x < 5, los posibles valores de la x pueden ser todos los numeros marcados con el circulo rojo, puede ser de cualquier color. En el examen de practica del nuevo examen del GED se incluye una pregunta con ese formato, pero con una desigualdad mas difícil.
Otros ejemplos usando este mismo método.
x > – 3
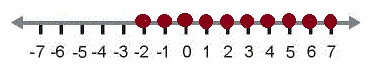
En los siguientes ejemplo vamos a usar el símbolo ≥, y el ejemplo nos indica que x es igual o mayor a tres, por eso marcamos también el tres. (Solo esta en rojo para destacar que se marca, no tiene que ir necesariamente de un color en particular).
x ≥ – 3

El siguiente ejemplo indica que el valor de la x es igual o menor a -1.
x ≤ – 1

Otro método, que puede parecer mas confuso, es el que usa cirulos negros y transparentes que se explica a continuación. (Si tienes dificultad para entender el MÉTODO II, procura dominar el MÉTODO I).
MÉTODO II
EJEMPLO I
x ≥ 2 (“x” es igual o mayor a dos)
PASO I
Dibuja un circulo negro sobre el número 2 de la recta numérica; el circulo negro indica que el valor de la «x» puede ser 2.
PASO II
Dibuja una fecha hacia la derecha que indica que el valor de “x” puede ser 2, 3, 4 o mayor.
Pista: si te confundes hacia donde dirigir la fecha solo asocia el símbolo de la desigualdad como una flecha > y dirigelo hacia esa dirección.
EJEMPLO II
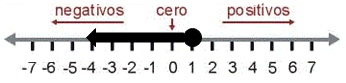
x ≤ 1 («x» es igual o menor a 1)
PASO I
Dibuja un circulo negro sobre el número -1
PASO II
Dibuja una fecha hacia la izquierda, (ojo, el símbolo de la desigualdad también apunta a la izquierda ≤ ) e indica que el valor de “x” puede ser 1, 0, -1, -2, etc.
EJEMPLO III
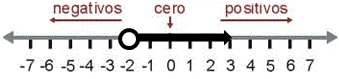
x > -2 (x es mayor a -2)
PASO I
Dibuja un circulo, transparente, en el -2 que indica que el valor de “x” NO PUEDE SER -2.
PASO II
Dibuja una fecha hacia la derecha (ojo, el símbolo > se dirige a la derecha) que indica que el valor de “x” NO ES -2, pero puede ser -1, 0, 1, 2, etc.
EJEMPLO IV
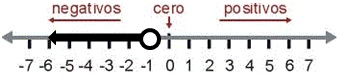
x < -1 ( “x” es menor a -1 pero no puede ser -1)
PASO I
Marca un circulo trasparente en el -1 para indicar que el valor de la “x” NO PUEDE SER -1.
PASO II
Dibuja una flecha hacia la izquierda, asocia el símbolo < que se dirige hacia la izquierda e indica que el valor de “x” NO ES -1 pero puede ser -2, -3, etc.
Ejercicios de práctica
Dibuja la recta de las siguientes desigualdades.
1. x ≤ 4
2. x > -3
3. x ≤ 0
4. x < – 2
Respuestas
2.
3.
4.
