Simplificación de radicales
Para entender un poco la simplificación de radicales hay que hacer una pequeña reseña de los exponentes y la raíz cuadrada, recuerda que si solo tenemos el signo de radical 
su índice es 2. En esos casos podemos usar sin problema las raíces cuadradas, por ejemplo 4, 9, 16, 25, 36, 49, 64, 81 y 100 son producto de la multiplicación de un número al cuadrado que quiere decir que su exponente siempre va a ser 2.
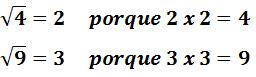
También es importante que aprendes las partes que forman un radical y ten presente que el ( • ) indica multiplicación
Un número elevado al cuadrado = x² (5² = 5 • 5)
Un número al cubo = x³ (5³ = 5 • 5 • 5 )
Un número a la cuarta potencia = x4 (54 = 5 • 5 • 5 • 5 )
Cuando un radical no es producto de un cuadrado perfecto, también se puede simplificar o expresar de una manera más simple, aunque si no estás familiarizado con la multiplicación y división, puede ser un poco complicado de entender. Además es indispensable que sepas los nombres y partes de un radical.
Vamos a saber que un radicar esta simplificado
- Cuando ya no se puede extraer ningún factor de él (división)
- Cuando no hay fracción bajo el signo radical
- Cuando el índice de la raíz no puede reducirse
EJEMPLOS I
El 32 no es una raíz cuadrada perfecta por tanto lo tenemos que simplificar usando la multiplicación y división.
PASO I
Identificar el índice del radical para después obtener un valor que sea un cuadrado perfecto. (En este caso el índice es 2, 
recuerda cuando es 2 no se escribe), (también puede ser un número al cubo, cuarta potencia, etc.).
PASO 2
Busca los factores, esto se te puede facilitar aplicando el método para obtener el máximo común divisor y de ahí buscar el número elevado al cuadrado. La forma de hacerlo es extraer el radicando e irlo dividiendo en números primos, empezando por el 2, si no es dividible entre dos hay que usar el 3, 5, 7, 11, 13, etc.
PASO 3
Como ya sabemos que nuestro índice es 2, identificamos el número que este elevado al cuadrado (4) y lo pasamos al lugar del coeficiente. Recuerda, el exponente del 4 es 2 que está representado por el índice del signo radical.
PASO 4
Puedes comprobar que tu respuesta esta correcta elevando el coeficiente (4) usando como exponente el índice del signo radical (2) y por último multiplicarlo por el radicando. 4² • 2 = (4 • 4 • 2) = 32
EJEMPLO 2
PASO I
Identifica el índice del radical, en este caso es (2) y vamos a buscar un número elevado al cuadrado.
PASO 2
Busca los factores esto se te puede facilitar aplicando el método para obtener el máximo común divisor y de ahí dentifica el cuadrado perfecto.
PASO 3
Como ya sabemos que nuestro índice es 2, identificamos el número que este elevado al cuadrado y lo pasamos al lugar del coeficiente. Recuerda, el exponente del 3 es 2 que está representado por el índice del signo radical.
PASO 4
Puedes comprobar que tu respuesta esta correcta elevando el coeficiente (3) usando como exponente el índice del signo radical (2) y por último multiplicarlo por el radicando. 3² • 2 = (3 • 3 • 2) = 18
EJEMPLO 3
PASO I
Identificar el índice de la raíz para obtener un número elevado al cubo porque el índice del radical es 3.
PASO 2
Busca los factores, esto se te puede facilitar aplicando el método para obtener el máximo común divisor y de ahí buscar un número elevado al cubo.
PASO 3
Como ya sabemos que el índice del radical es 3, identificamos el número que este elevado al cubo (23 ) y lo pasamos al lugar del coeficiente. Recuerda, el exponente del 2 es el 3 y está representado por el índice del signo radical.
PASO 4
Puedes comprobar que tu respuesta esta correcta elevando el coeficiente (2) usando como exponente el índice del signo radical (3) y por último multiplicarlo por el radicando. 2³n 2 = (2 • 2 • 2 • 2 = 16
EJEMPLO 4
PASO I
Identificar el índice de la raíz para obtener un número elevado a la cuarta potencia porque el índice de la raíz es 4.
PASO 2
Busca los factores, esto se te puede facilitar aplicando el método para obtener el máximo común divisor y de ahí buscar un número elevado a la cuarta potencia.
PASO 3
Como ya sabemos que el índice del radical es 4, identificamos el número que este elevado a la cuarta potencia (34 ) y lo pasamos al lugar del coeficiente. En este ejemplo ya tenemos un coeficiente (2), solo pasamos a la parte de afuera el otro coeficiente multiplicando (2 • 3).
PASO 4
Multiplica ambos coeficientes 2 • 3 = 6 y representa tu respuesta.
PASO 5
Comprueba tu respuesta elevando el coeficiente (6) usando como exponente el índice del radical (4) y por último multiplícalo por el radicando.
64 • 3 = (6 • 6 • 6 • 6 • 3) = 3888.
Si resuelves la expresión inicial , elevando el 2 a la cuarta potencia y multiplicándolo por 243, podrás ver que te da la misma respuesta.
24 • 243 = (2 • 2 • 2 • 2 • 243) = 3888.
EJERCICIOS DE PRACTICA
RESPUESTAS
