Suma de Fracciones
Para sumar fracciones vamos a identificar primero dos tipos de fracciones, las homogéneas que tienen el mismo denominador y las heterogéneas que tienen diferente denominador.
Las fracciones homogéneas se suman los numeradores y el denominador se recorre, es necesario simplificar si se requiere expresando el resultado en número mixto, entero o fracción propia.
Ejemplos I
Se suman los numeradores 1+ 2 = 3 y el denominador se recorre.
Ejemplo II
Se suman los numeradores 3 + 1 = 4, al pasar el denominador queda cuatro cuartos que es igual a un entero. Siempre que se tiene el mismo número como numerador y denominador es un entero.
En la suma de fracciones heterogéneas (diferente denominador) se usan métodos diferentes dependiendo de su país de origen.
PRIMER MÉTODO
Se busca el mínimo común múltiplo (m.c.m.) que es el número que puede ser divisible entre ambos denominadores.
- Si el denominador mayor es divisible entre el otro denominador se puede usar como mínimo común múltiplo
- Si son números chicos se puede obtener multiplicándolos los denominadores.
PASO I
Se busca el m.c.m. En el primer ejemplo es 15.
PASO II
Se divide el m.c.m. entre el denominador de la primera fracción y se multiplica por el numerador. (15 ÷ 3 x 1 = 5).
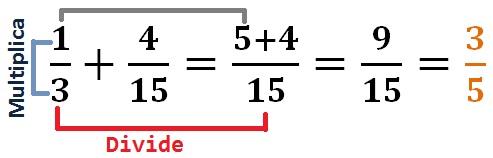
PASO III Para simplificar se busca un número que divida al numerador y denominador sin dejar residuo.
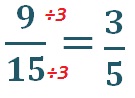
SEGUNDO MÉTODO
Este método se amplía las fracciones para tener fracciones homogéneas.
PASO I
Para tener el mismo denominador hay que convertir una o dos fracciones en fracciones homogéneas. (Generalmente se obtiene buscando un numero que multiplicado nos dé el mismo denominador)
Para obtener el mismo denominador hay que buscar un número que multipicado por el denominador nos de 6 y ese mismo número lo multiplicamos por el numerador.
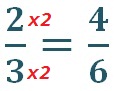
PASO II
Substituye la fracción, suma los numeradores y pase el denominador
PASO III
Si es necesario, simplifica el resultado. Fracciones impropias se convierten a números mixtos.
EJERCICIOS DE PRACTICA
Resupestas y procedimiento del primer método
