Para entender la factorización vamos a definir los conceptos y mostrar ejemplos sencillos para después elaborar operaciones más avanzadas. Primero, un “factor” es cada uno de los números que se multiplican para formar un producto, podemos decir que es la operación opuesta a la multiplicación.
Podemos ilustrar esa explicación buscando todos los posibles factores del 12.
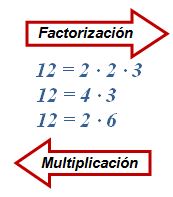
En otras palabras (2) (2) (3) = 12, por lo que los factores de 12 son 2, 2, 3, o dependiendo los factores que necesitemos podemos usar el 4 y 3, etc.
Veamos otros ejemplos:
(3) (5) = 15 por lo que los factores de 15 son 3 y 5
(2) (3) (7) = 42 por lo que los factores de 42 son 2, 3 y 7
(5) (7) = 45 por lo que los factores de 45 son 7 y 5
Factor común
Cuando un número entero divide exactamente a dos o más números dados sin dejar un residuo le llamamos “factor común”, para ilustrar este ejemplo hay que buscar los factores de 6, 10 y 30.
6 = (2)(3)
10 = (2)(5)
30 = (2)(3)(5)
En los ejemplos anteriores nuestro “factor común” es el 2 porque cada uno de estos números es divisible entre 2 y no deja residuo.
Para poder obtener los factores de una expresiones algebraicas donde ya se incluyen literales (letras) hay que entender y dominar estos conceptos primero usando números. Puedes llevar a cabo los siguientes ejercicios.
Obtén los factores y el “factor común” de las siguientes cantidades.
- 6, 9
- 45, 20,
- 36, 15, 12
- 40, 8, 12
- 21, 9, 15
- 49, 21, 35
- 25, 20, 30
RESPUESTAS
- (2)(3) = 6 / (3)(3) = 9 – factor común = 3
- (3)(3)(5) = 45 / (2)(2)(5) = 20 – factor común = 5
- (2)(2)(3)(3) = 36 / (3)(5) = 15 / (2)(2)(3) = 12 – factor común = 3
- (2)(2)(2)(5) = 40 / (2)(2)(2) = 8 / (2)(2)(3) = 12 – factor común = 2
- (3)(7) = 21 / (3)(3) = 9 / (3)(5) = 15 – factor común = 3
- (7)(7) = 49 / (3)(7) = 21 / (7)(5) = 35 – factor común = 7
- (5)(5) = 25 / (2)(2)(5) = 20 / (2)(3)(5) = 30 – factor común = 5

Factor es de 45 son 3×3×5
Factor es de 45 son 3×3×5
Simplificado es 3 a la raiz cuadrada por 5.
Creo que se equivoco.sorry.
¿a qué te refieres?
¿a la forma en que se expresa la factorización de 45 para encontrar el factor común? La actividad es encontrar el factor común, no simplificarlo, y lo exprese (3)(3)(5) para que los estudiantes identifiquen los factores, porque hay muchos que tienen dificultades incluso con las tablas, pero no se si a eso te refieras.
Es un poco complicado para
Es un poco complicado para esto del factor común pué solo llegue a sexto de primaria consejos por favor
Poco a poco
Anita, es normal que los sientas complicado y debes darte tiempo, con la practica cuando menos te des cuenta vas a ir entendiendo. Antes de estudiar estos temas trata de familirizarte con la multiplicación, y si quieres factorizar de manera sencilla simplemente identifica los números que estas multiplicando. Por ejemplo 2 x 3 = 6, los factores de 6 son 2 y 3. Otro ejemplo 2 x 7 = 14, los factores de 14 son 2 y 7. Ya cuando domines cantidades sencillas ve intentando con números mas grandes, por ejemplo 20 es un número chico pero puede tener mas factores, 2 x 2 x 5 = 20; y también 4 x 5 = 20. Solo practica buscando la multiplicación invertida.
Ayuda !!
De favor me podrian dar info acerca de algún libro de practicas, de matematicas lo más actual que tengan por favor .
gracias .
Material
Aquí explico lo relacionado con los libros y el material que pueden usar.
hola gracias por explicar
hola gracias por explicar todos los temas muy bien
Gracias Irene
Me da gusto leer tu comentario 😀 saludos!!
Lista para esta nueva
Lista para esta nueva oportunidad
Siempre hay oportunidades!!
¡Qué tal Delmis!, así es, siempe hay nuevas oportunidades para los que saben aprovecharlas. Saludos!!
tengo una duda
¿como puedo dividir las factorizaciones con la coma es lo que no entendi a mi tarea pero nesesito una respuesta de ayuda por ejemplo:
12 , 6 es el que no entiendo bien pero si me dieran una respuesta para que me apurara a mi tarea
Simbolos
Soii, en tu comentario salen solo simbolos, no entiendo bien tu pregunta porque no distingo los números.