Un monomio está compuesto por un solo término el cual incluye signo, coeficiente, incógnita y exponente por tanto un polinomio es aquel que tiene dos o más términos. Para factorizar un polinomio vamos a seguir los siguientes pasos:Si tienes dificultad con estos temas es recomendabel revisar primero:– Concepto de factorización– Máximo común factor– División de polinomios
Ejemplo I
b2 + 3b
PASO I: Buscar el factor común de ambos términos. El factor común para las incógnitas (letras) es la que se encuentra en ambos términos. Para entender el factor común de los coeficientes (números) revisa este enlace.
Para este caso el factor común es la “b”
PASO II: Dividir cada termino entre el factor común que se encontró, ósea que vamos a dividir b2 ÷ b y 3b ÷ b. Si tienes dificultad para dividir términos, revisa este enlace.
b2 ÷ b = b
2b ÷ b = 2
PASO III: Se escriben las respuestas dentro de un paréntesis incluyendo los signos, y afuera del paréntesis se escribe el factor común.
b (b + 2)
Ejemplo II
10n – 30mn2
PASO I: Buscamos el factor común para las incógnitas (letras) y los coeficientes (números)
10 → 2, 5, 10
30 → 3, 10
n – mn2 → n
Nuestro factor común va a ser el 10 porque se repite en ambos coeficientes y la n
OJO: Si al factorizar se repite más de dos veces un número escogemos el MAYOR como factor común
PASO II: Dividimos los términos entre los factores comunes
10n ÷ 10n = 1
– 30mn2 ÷ 10n = – 3mn
PASO III: Poner las respuestas que obtuvimos de las divisiones dentro de un paréntesis respetando signos y afuera el factor común que obtuvimos
10n(1 – 3mn)
Ejemplo III
15x3 + 20x2 – 5x
PASO I: Obtenemos el factor común de los coeficientes y las incógnitas
15 → 3, 5
20 → 2, 4, 5, 10
5 → 1, 5
Factor común → 5
Para las incógnitas es x
PASO II: Dividimos cada termino entre el factor común
15x3 ÷ 5x → 3x2
20x2 ÷ 5x → 4x
– 5x ÷ 5x → -1
PASO III: Escribimos las respuestas de la división dentro de un paréntesis incluyendo los signos y afuera el factor común.
5x (3x2 + 4x – 1)
Ejercicios de práctica
- 8x2 + 12xy
- m2 + m
- p3 – p5 – p7
- 35x2y3 – 70x3
- xy – yz
- 5c2 + 15c3
- 2b2c + 6bc2
- 4m2 – 8m + 2
Respuestas
- 4x(2x + 3n)
- m (m+1)
- x3 (1 + x2 – x4)
- 35x2(y3 – 2x )
- y(x –z)
- 5c2(1 + 3c)
- 2bc(b + 3c)
- 2(2m2 – 4m + 1)

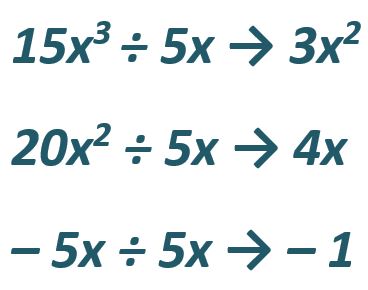
Factorizacion de polinomios
En mi opinion una forma mas sencilla de factorizar los polinomios es
mediante el metodo Aspa simple.
aspa trinomios
Si ese es sencillo pero se aplica a trinomios, estos casos no son trunomios.
Yo siempre que voy a factorizar lo primero que hago es contar cuantos términos hay en mi expresión y después comienzo a descartar los métodos que no cuadran con los términos que se me presentan.
Por ejemplo, si en la expresión hay dos términos, se puede factorizar a través de factores comunes, diferencia de cuadrados, suma o restas de expresiones cubicas y también por medio de términos elevadas a la misma potencia.
Si son tres, a través del trinomio cuadrado perfecto, factor común, de la forma x2-x-+c, etc.
saludos, familia ged
Muy buena aportación Enrique, gracias. ¡¡Saludos!!!