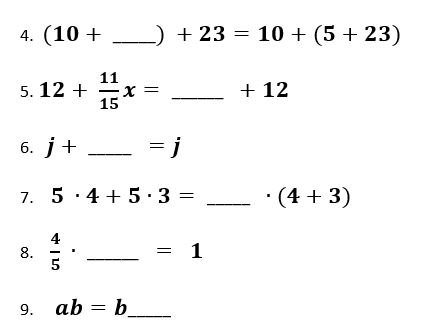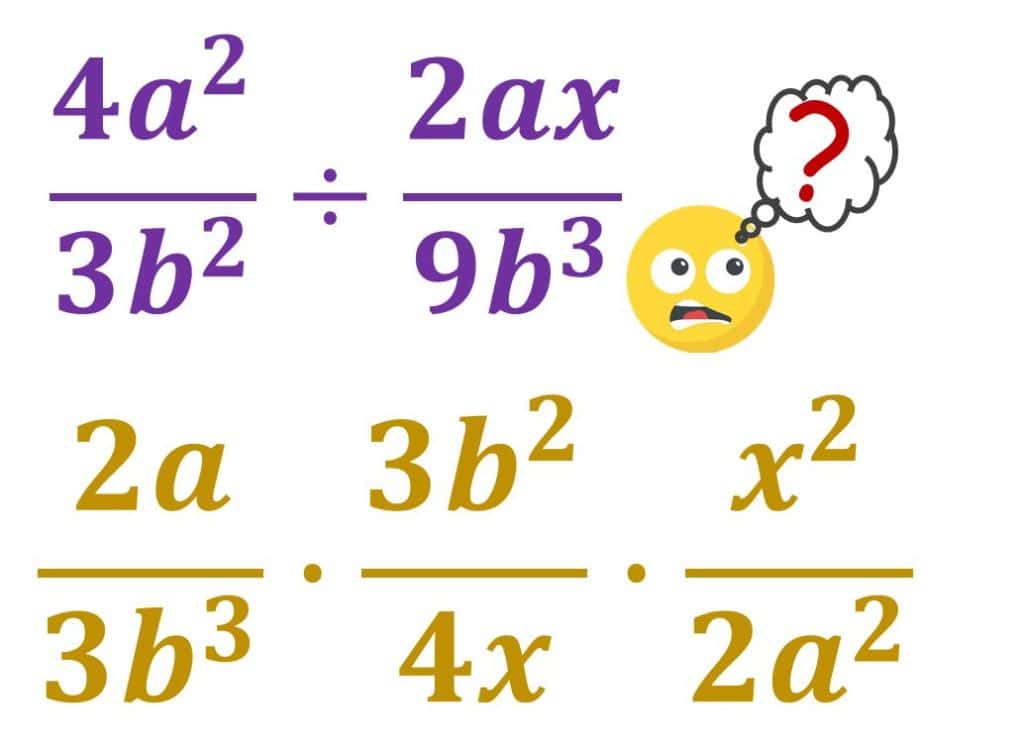álgebra
Examen de practica – álgebra
https://youtu.be/urwXJw8wdp8 1. La presión arterial sistólica es la presión máxima producida por cada latido del corazón. Tanto la presión arterial baja como la presión arterial alta pueden ser motivo de preocupación médica. Por lo tanto, los profesionales de la...
Problemas de varios pasos y propiedades de los números reales
https://youtu.be/RzHsoVt_Wqw Pregunta 1 a la 3 son en referencia a la siguiente información: Una camioneta turística de San Diego comienza su recorrido en Coronado Island, se detiene en SeaWorld, luego en el Wild Animal Park y finalmente regresa a Coronado...
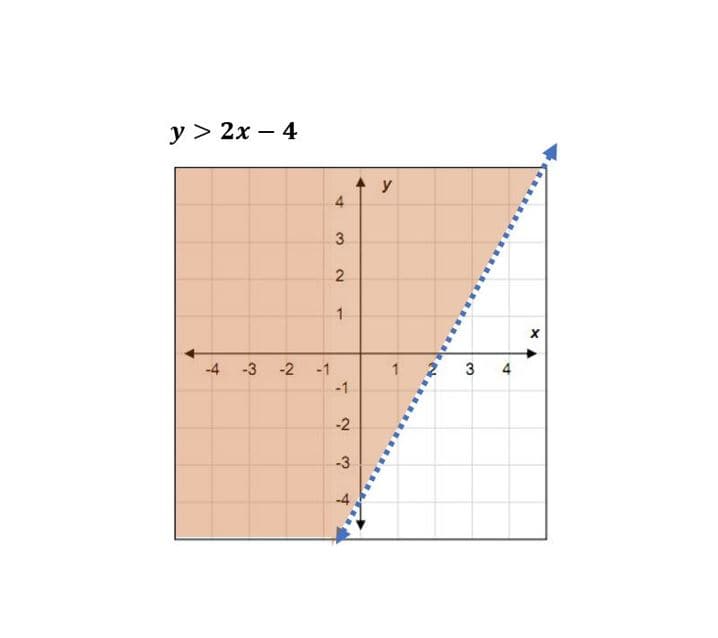
Inecuaciones lineales con dos variables
En este capítulo vamos a revisar como resolver las inecuaciones con dos variables y graficarlas en el Plano Cartesiano. Para ello es importante que se tengan los siguientes conocimientos previos: Plano Cartesiano Pendiente en una recta Métodos para obtener la...
Problemas verbales- ecuaciones lineales
https://youtu.be/Kr0-jSkNWLM 1. Un bacteriólogo quiere determinar la cantidad de microrganismos contenida en la piel antes de limpiarla. Identifica que la cantidad de microorganismos en, y miligramos, por cada centímetro cuadrado de la piel dependía del grosor de...
Problemas verbales – álgebra
https://youtu.be/FozTM8CdEAc 1. Adela salió de compras, en la primera tienda gasto $13 dólares y al momento de entrar a la segunda tienda llevaba $65 dólares. a) 13 - x = 75 b) 75 = x - 13 c) x - 13 = 75 d) x + 13 = 75 2. Laura ahorro ¾ de su aguinaldo. Si su...
Problemas verbales de álgebra
Los siguientes problemas están ordenados por nivel de complejidad. https://youtu.be/UgmV_Q1pQF4 EXPRESIONES 1. Cinco veces un número aumentado a la mitad de otro número. 2. La familia Gómez quiere comprar un paquete de excursión al...
Examen de practica -ÁLGEBRA
Si te estás preparando para tu examen del GED, HiSET o TASC, este examen de practica te puede ayudar para auto-evaluarte y determinar que áreas y temas debes estudiar mas. Al final de las preguntas vas a encontrar un video con las respuestas y explicación de cada...
Clase de álgebra básica
La siguiente clase esta dirigida a estudiantes adultos que quieren aprender lo básico de álgebra y avanzar poco a poco hasta tener las bases para estudiar contenidos mas avanzados. La clase se va a impartir los LUNES a las 8:00 pm hora este por el canal de Youtube...
13ª CLASE DE ÁLGEBRA – Problemas verbales de ecuaciones simultáneas
CLASE ANTERIOR Aquí puedes suscribirte al canal de YouTube (solo dale click a la imagen) https://youtu.be/O-BRj2Tms5I https://youtu.be/XGYw4H_cc6s https://www.spanishged365.com/sistema-de-dos-ecuaciones/ EJERCICIOS DE PRACTICA La...
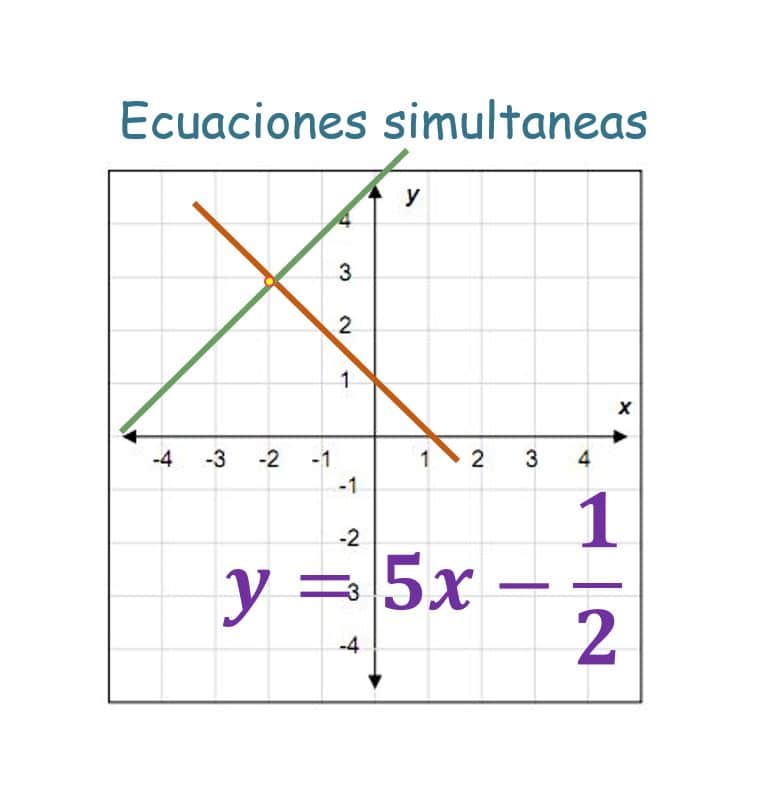
12ª CLASE DE ÁLGEBRA – ecuaciones simultaneas
CLASE ANTERIOR SIGUIENTE CLASE Durante este verano 2019 las clases se van a impartir los jueves a las 8:00 pm hora este y los sábados a las 10:30 am hora este por el canal de YOUTUBE, una vez que se termine la clase vas a encontrar las tareas y el video publicado...
11ª CLASE DE ÁLGEBRA – multiplicación y división de fracciones
CLASE ANTERIOR SIGUIENTE CLASE Durante este verano 2019 las clases se van a impartir los jueves a las 8:00 pm hora este y los sábados a las 10:30 am hora este por el canal de YOUTUBE, una vez que se termine la clase vas a encontrar las tareas y el video publicado...
10ª CLASE DE ÁLGEBRA- mcd y mcm en expresiones algebraicas
CLASE ANTERIOR SIGUIENTE CLASE Durante este verano 2019 las clases se van a impartir los jueves a las 8:00 pm hora este y los sábados a las 10:30 am hora este por el canal de YOUTUBE, una vez que se termine la clase vas a encontrar las tareas y el video publicado...