La pendiente en algebra es la inclinación de una recta representada en el plano cartesiano y es necesaria para resolver las ecuaciones lineales planteadas con la fórmula:
y = mx + d
Las preguntas relacionadas con la pendiente pueden variar mucho y presentárselas en diferente formato por lo que es importante que aprendan a obtenerla e identificarla usando los siguientes métodos.
1. Aplicando la fórmula
2. Obtenerla viendo las coordenadas
3. Usando el plano cartesiano
4. Identificarlas en las funciones
De los métodos anteriores ya deben estar familiarizados con el primero y el tercero, ese tema se explica en “pendiente”, entender ese tema les va a facilitar la siguiente explicación.
PRIMER MÉTODO
La fórmula puede parecer el más difícil de los cuatro ya que deben dominar las operaciones de números con signo, coordenadas en el plano cartesiano, fracciones y sustitución de valores.
Si tenemos las siguientes coordenadas m (3, 4) n (1, 0) y sabemos que la fórmula es:
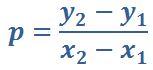
Paso I
Asignar valores de las variables (letras) que estan en la fórmula a las coordenadas y nos quedan de la siguiente manera: (Hay que tenerpresente que el primer número de cada coordenada representa las «x» y el segundo siempre va a representar las «y»).
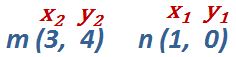
Paso II
Sustituir valores aplicando la fórmula y resolvemos.
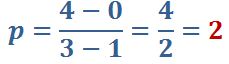
SEGUNDO MÉTODO
En la medida en que se familiaricen y resuelvan sin problema la fórmula de la pendiente van a tener la habilidad de obtenerla solo viendo las coordenadas y sin aplicar la fórmula. Digamos que lo hagan mentalmente y eso requiere práctica y sobre todo dominio de las operaciones de números en signos.
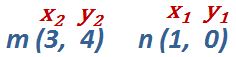
La mejor forma de aplicar este método es visualizar los valores mentalmente y tener presente que solo deben restar y al final solo simplifican o dividen la fracción.
La parte difícil se va a presentar cuando se presenten valores negativos, analicen los siguientes ejemplos y vean como los signos cambian el valor de la pendiente.
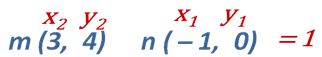
La operación mental que debes hacer es 4 – 0 y 3 – – 1 te queda 4/4 y eso es = 1
Recuerda, es siempre – – 1 porque un signo es de la fórmula y otro es el del – 1 y cuando tenemos dos signos negativos juntos se multiplican.
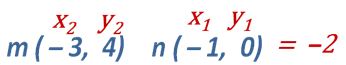
La operación mental que debes hacer es restando las «y» es 4 – 0 y restando las «x» – 3 – – 1 = 4/–2 = – 2
Si esto te parece confuso intenta repasar los siguientes temas: de SUMA Y RESTA DE NÚMEROS CON SIGNO y MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS CON SIGNO.
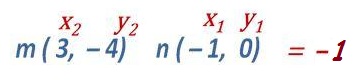
La operación mental que debes hacer es restar las «y» – 4 – 0 = – 4 y restar las «x» 3 – – 1 = 4 al acomodar – 4/4 = -1
Para desarrollar esta habilidad no hay más que practicar y tratar de hacerlo lo más rápido y asertivamente posible, esto te va a permitir contestar en menor tiempo.
TERCER MÉTODO
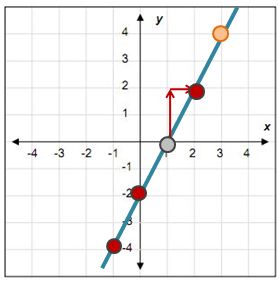
Identificar la pendiente en el plano cartesiano cuando te presentan una recta numérica donde no necesariamente se te van a indicar las coordenadas como el ejemplo siguiente:
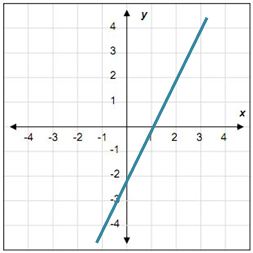
PASO I
Visualizar las coordenadas, que son los puntos donde se cruzan los puntos y atraviesa la recta.
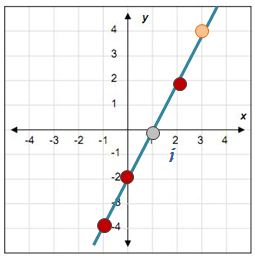
PASO II
Elegir un par de coordenadas y aplicar el método para obtener la pendiente visualizando un triángulo rectángulo. Se cuentan las unidades (cuadros en y) y las unidades en x. Se representan en forma de fracción poniendo el valor en «y» en el lugar del numerador y el de «x» en el lugar del denominador.
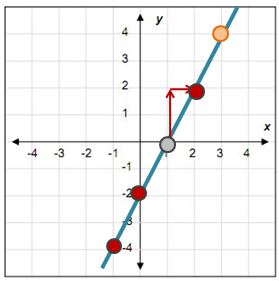
PISTA: Se puede usar cualquier par de coordenadas y la respuesta va a ser siempre la misma.
CUARTO MÉTODO
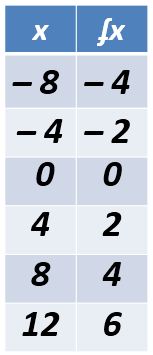
Otra forma de identificar la pendiente es en las funciones que es la representación de las coordenadas en una tabla o relación de datos. En el siguiente ejemplo usamos las coordenadas de la imagen anterior, solo se escriben en la columna de la izquierda los valores de “x” y en la derecha el valor correspondiente a “y”. También es posible que en lugar de la «y» este el símbolo ʄx que indica que esos datos son una función en «x».
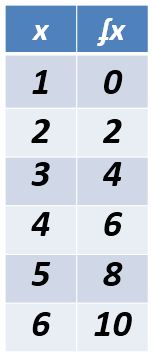

Si pones atención puedes identificar que el cambio en “y” representa la pendiente que en la imagen anterior es «2», solo hay que tener presente que siempre que el cambio en la relación de«x» se de uno en uno, la «pendiente» va a ser el cambio que esta representado en «y» o ʄx.
Si solo te presentan una función, como el caso anterior, no es necesario aplicar la fórmula de la pendiente. Solo hay que identificar la diferencia entre un número y otro en la columna de las “y”, esa es la pendiente. De hecho, puede haber problemas donde este método facilite la solución de la fórmula y = mx + d, donde “m” representa la pendiente.
Ahora, en caso de que el cambio en «x» no sea de uno en uno, solo tienes que identificar el cambio que hay en la relacion de «y», lo escribes en el lugar del numerador, después identifica el cambio en «x» y lo escribes en el lugar del denominador. Como se esta representando en forma de fracción. Algunas veces va a ser necesario simplificar o dividir.
Practica con el siguiente ejemplo, primero identifica el cambio en «x», si va de dos en dos, de tres en tres, de cinco en cinco, etc.
Una vez que lo identifiques escribelo en el lugar del denominador.
Después identifica el cambio en «y» y escribelo en el lugar del númerador.
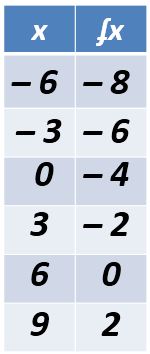
En este ejemplo tu pendiente debe ser 2/3 porque el cambio en «y» es de dos en dos y el cambio en «x» es de tres en tres.
Ahora hay que obtener la pendiente con este otro ejemplo:
En este caso hay que simplificar después de obtener los cambios te debe quedar 2/4 y esta respuesta hay que simplificarla (si no sabes como simplificar, revisa este tema) y la respuesta final debe ser ½.
Últimos tips, siempre que los valores en «y» sean de cero en ambas coordenadas, no hay pendiente y finalmente hay que tener presente que si la pendiente es negativa, es un poco mas difícil identificar el signo solo con los cambios en las relaciones de «x» y «y» pero se puede comprobar haciendo la operación mentalmente o aplicando la fórmula.
EJERCICIOS DE PRACTICA
Con los siguientes pares de coordenadas, obten la pendiente aplicando esos cuatro métodos, en todos te debe dar el mismo resultado y en las funciones pueden intentar por lo menos encontrar cinco coordenadas diferentes.
- (5, 2) (3, 1)
- (9, 5) (4, 2)
- (6, 5) (5, 0)
- (8, 0) (6, 0)
- (3, 9) (2, 3)
- (– 4, 2) (– 5, 3)
- (2, – 4 ) (0, – 6)
- (– 1, – 4) (5, – 3)
- (0, – 3) (– 2, – 5)
- (– 3, – 7) (– 2, – 4)
RESPUESTAS
- ½
- 3/5
- 5
- No hay pendiente
- 6
- – 1
- 1
- 1/6
- 1
- 3

gracias
super estos ejemplos gracias.
🙂
Y es importante aprender los cuatro métodos, no se sabe cual puede ser útil al momento del examen. Saludos!!
MUCHAS GRACIAS
Exelente explicacion…. Ahora ya me quedo mas claro, la verdad si lo necesitamos mucho por que en el examen viene varias preguntas relacionadas con estos temas… Es muy importante tener presente que ahi varias formas de resolverlas..
Gracias
Un gusto!!
Me da gusto Guadalupe y mas saber que hay personas que estudian y usan estos recursos. Saludos!!
pregunta
Hola. Me gustaria pedirle de favor me explicara, el ejercicio # 7 y 9. Ya que me salen resultados diferentes.
Pendiente
Creo que tu error va a estar al aplicar el signo negativo de la formula y el signo negativo de la coordenada, porque se escriben ambos y se multiplican, ejem. 2 – – 4 = 6 o -7 – – 4 = -3, revisa el video de este tema te va a quedar más claro.
Hola buen dia me interesa
Hola buen dia me interesa saver como resolviste con la formula este ejercicio porfa1. Marcos trabajo 30 horas esta semana y gano a $7.50 por hora. Su amigo Andrés gano a $9.00 por hora ;Cuántas horas debió trabajar Andrés para igualar el ingreso de Marcos en 30 horas?
Multiplicar y dividir
Solo tienes que multiplicar el número de horas que trabaja Marcos por su paga que es $7.5 y paga saber cuantas horas tiene que trabajar Andres ganando lo mismo, divides ese resultado entre $9 que es lo que le pagan a Andres.
Disculpe si al primer metodo el resultado es una fraccion que se puede simplicar como 2/4
La simplifico o lo dejo asi
Se debe simplificar 😉
La 9 es 1 positivo verdad?
Si Vero, tienes razón, es positivo. ¡Gracias!! :>