Una vez que se ha aprendido a multiplicar términos representados en monomios o binomios se puede iniciar con la multiplicación de factores con dos términos. Para ello es importante dominar la ley de signos para suma y resta y para multiplicación y división, de lo contrario puede crear confusión. De igual manera, hay que tener presente que la multiplicación en algebra puede representarse de la siguiente manera, los primeros tres son los más usados.
- 2x
- 2(x)
- 2 • x
- 2*x
A continuación tenemos dos factores, cada uno con dos términos, (x + 5) (x – 4). Para resolverlo, los dos términos del primer factor (x + 5) multiplican los dos términos del segundo factor (x – 4). Puede haber varios métodos para resolverlo, pero veamos el más sencillo aplicando el siguiente orden:
EJEMPLO I
(x + 5) (x – 4)
PASO I
Multiplicar los términos de los factores en el orden que se indica.
x (x) = x2
x (– 4) = – 4x
5 (x) = 5x
5 (–4) = – 20
PASO II
Hay que escribirlos en el orden en que se multiplican.
x2 – 4x + 5x – 20
PASO III
Simplificar sumando o restando términos semejantes, en este caso el – 4x y 5x se restan. Nos da x.
PASO IV
Se escriben todos los valores juntos. (La «x» al cuadrado, la «x» sola y el coeficiente).
x2 + x – 20
EJEMPLO II
(x – 3) (6 + x)
PASO I
Multiplicar los términos de los factores en el orden que se indica.
x (6) = 6x
x (x) = x2
–3 (6) = –18
–3 (x) = –3x
PASO II
Se escribe primero el que tienen potencia 2; segundo, los que tienen literales con potencia 1; al final el coeficiente (número).
x2 – 3x + 6x – 18
PASO III
Simplificar sumando o restando términos semejantes – 3x + 6x = 3x
x2 + 3x – 18
EJERCICIOS DE PRACTICA
1. (x – 4) (x – 2)
2. (a + 2) (3 – 3a)
3. (5z + 1) (z – 3)
4. (2a – 3) (a + 4)
5. (y – 2) (y – 8)
6. (x + 1) (x + 7)
7. (6x + 4) (3 – 2x)
8. (m – 9) (m – 9)
9. (4n + 6) (n – 2)
10. (7 + b) (b – 3)
RESPUESTAS
1. x2 – 6x + 8
2. – 3a2 – 3a + 6
3. 5z2 – 14z – 3
4. 2a2 + 5a – 12
5. y2 –10y + 16
6. x2 + 8x + 7
7. – 12x2 + 10x + 12
8. m2 – 18m + 81
9. 4n2 – 2n – 12
10. b2 + 4b – 21

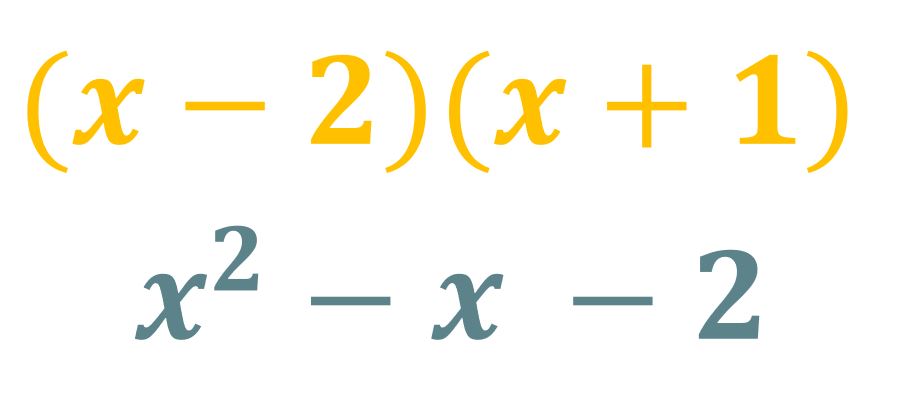
en el problema numero dos
en el problema numero dos estoy un poco confundida con la respuesta me podria explicar porfavor?
Factores
Te creo confusión por el símbolo ª la computadora los pone automáticamente, tengo que poner atención para borrarlos. Fíjate si te queda claro una vez que quite ese símbolo, si no me haces saber. El orden puede de la respuesta no importa, pero se recomienda ponerlo en el orden de las potencias.
Respuesta de el problema #4
En el problema 4 es (2a-3)(a+4) la Respuesta sale una (z) de Donde???
Mi error
No, no, es "a" fue mi error al escribirla, ya esta editada.
Hola, felicidades por su
Hola, felicidades por su pagina ayuda bastantisimo, mi pregunta es cuantas oportunidades hay para cada examen?? Por que unas personas me dicen que son 6 pero Otras me dijeron que son 3 nadamas yo vivo en Elgin il.
Oportunidades
En Illinois no puedes repetir una hasta que no hayas presentado todas, a reserva de que interprete mal. Si ya hiciste dos veces un examen, no te dejan hacerlo hasta despues de 60 días para que tengas tiempo de prepararte mejor y hasta donde se son seis veces al año pero independientemente del número de veces, creo que si no se pasa un examen, es mejor prepararse por lo menos unos tres meses, quizas no se necesiten las 6 oportunidades.
Ejercicio 8
Hola! Me puedes ayudar con el problema 8? Los nueve se suman o se multiplican? mi resultado fue m"-m18-81
Gracias!!
Estas bien
Si, tu respuesta es correcta, solo que la m va después del 18 y el 81 es positivo porque se multiplican primero los signos (-) (-) = +
muy bueno
muy buenos ejenplos, gracias me estan yudando mucho
🙂
Me da gusto 😉 Saludos!!
Quisiera preguntar SI en
Quisiera preguntar SI en ciencias, Te Dan Las formulas en Una hoja o Te Las tienes q aprender de memoria?
Formulas
Hay formulas predeterminadas que van a poder ver en la pantalla de la computadora, sin embargo para ciencias puede haber problemas que impliquen formulas diferentes, lo mas seguro esque se las incluyan en el problema y ustedes tendrían que sustituir los valores y resolver. Recuerda que para ciencias, sociales y matemáticas deben llevar la calculadora.
EJEMPLO 1
Perdona, en el ejemplo 1 la parte 3 no entiendo de donde salen tantas X ? gracias
Ejemplo 1
Incorporé el paso 4 para explicar la suma y resta de las "x"