En la multiplicación de radicales hay que estar familiarizado con la simplificación para que se faciliten las operaciones. Una de las características importantes es que al multiplicar los radicales estos deben tener el mismo índice aunque el radicando y el coeficiente sean diferentes. También puede ser posible simplificar antes de multiplicar, lo que hace la operación más sencilla. Veamos los ejemplos:
EJEMPLO I
PASO I
Multiplicar los coeficientes 3 • 4 y los radicandos 5 • 2.
EjEMPLO II
Multiplicar después simplificar
PASO I
Multiplicar los coeficientes (3 x 4) y los radicandos (20 x 18)
PASO II
Simplificar el radicando 360
PASO III
Pasar los números elevados al cuadrado hacia afuera (en el lugar del coeficiente) y dejamos los números que no tienen ningún exponente.
PASO IV
Multiplicar los coeficientes (12 • 2 • 3) y los radicandos (5 •2)
Otro método para resolver la multiplicación es simplificar antes de multiplicar. Veamos el mismo problema
Simplificar antes de multiplicar
EjEMPLO III
Simplificar radicandos y después multiplicar
PASO I
Multiplicar los coeficientes
PASO II
Simplificar los radicandos (20 y 18) 20 = 2•2•5 y 18 = 2•3•3
PASO III
Ya que nuestro índice es 2, hay que identificar los números que se repitan dos veces y por tanto se puedan elevar al cuadrado. (Estos son el 2 y el 3)
PASO IV
Pasar los números elevados al cuadrado hacia afuera (en el lugar del coeficiente) y dejamos los números que no tienen ningún exponente.
PASO V
Multiplicar los coeficientes (12 • 2 • 3) y los radicandos (5 •2)
En algunos ejercicios puede ser más fácil simplificar los radicandos antes de multiplicar, como en el siguiente ejemplo.
Ejemplo IV
PASO I
Multiplicar los coeficientes.
PASO II
Simplificar los radicandos (24, 54 y 375) y expresar los contenidos en la parte del radicando.
PASO III
Ya que nuestro índice es 3, hay que identificar los números que estén elevados al cubo ósea la tercera potencia y ponerlos en el lugar del coeficiente dejando adentro los que no tienen ninguna potencia.
PASO IV
Pasar en el lugar del coeficiente los números que esten elevados al cubo. Se deja los números sin potencia en el lugar del radicando.
PASO V
Multiplicamos los coeficientes (30 • 2 • 3) y los radicandos (3 • 2 • 3)
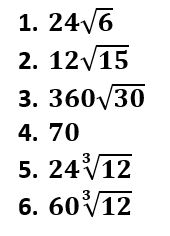

TENGO UN DUDA
hola maestra , muchas gracias por los ejercicios me han servido mucho , pero el ejercicio 4 no me sale me podria poner el procedimiento porfavor (:
Radicales
Aplica el paso 2 del ejercicio IV, una vez que simplifiques pasas afuera los números que se repiten dos veces y van a ser el 7 y el 5, dejas adentro los números que sobren y son 2 y 2, estos quedan dentro del simbolo de radical, por último multiplicas ambos.
Aljebra
Podrian poner mAs ejercicios de aljebra estoy frustada no he pasado el examen de matematicas se low agradeceria lily
Algebra
Si ya aprendiste todos los temas que estan en la pagina, solo falta agregar lo relacionado con la formula cuadratica, trinomios cuadrados, factorización y funciones, esos temas los voy a ir incorporando pronto.
Ayuda
En el paso II donde dice simplificar, como saco el 20 y 18?
preguntas de practica
Esos datos son parte del ejercicio solo pones los dos radicandos que son el 20 y 18, y afuera dejas el 3 y 4 estos ultimos los multiplicas, y los radicandos los simplificas como se muestra en el paso II
ejercicio 4
este ejercicio esta interesante.
No se puede simplificar mas la raiz cuadrada de 4? es decir 2 por 2
y el resultado final seria 35 por 2 = 70
O en que estoy mal?
El ejercicio 4 no queda radical.
Es exacta, la respuesta es 70
Si Maritza, la respuesta es 70.
Radicales
Si puedes obtener la raíz cuadrada de 4 y expresarlo en 70 dependiendo que tipo de operación tengas que hacer, si solo te piden resolver esa multiplicación lo mas correcto es el 70; si tienes que simplificar para continuar con otras operaciones como suma o resta de radicales semejantes y el radicando debe ser 4 u otro número, hay que expresar el radical en esa forma.
como saco el 20 y el 18 en el ejemplo II
en el ejemplo II no entiendo como saca el 20 y el 18
El 20 y 18
Hola Laura, esos números son parte de la pregunta, en el ejemplo II y III se usan las mismas cantidades para explicar dos formas diferentes de resolverla.
Hola, yo tengo 2 dudas, la
Hola, yo tengo 2 dudas, la primera es en el ejercicio 4, usted dice q dejemos afuera los numeros q se repiten, q seria el 5 y el 7, y adentro el 2 y 2, pero es q el 2 tambien se repite, como sabriamos q el 2 va adentro cuando tambien se repite?
Y mi segunda duda es en el ejercicio 6, no me sale, porq descompuse el resultado de la multiplicacion q fue 2592000, y me salio afuera 2x2x3 y adentro 2x2x5x5x3, pero al multiplicarlo no me da el mismo resultado q a usted, me lo podria explicar xfavor….muchas gracias
Radicales
Creo que un ejemplo que puede ayudarte para entender cual poner afuera es la raíz cubica (3) de 16, al encontrar los mcm 2x2x2x2=16 pero como quieres la raíz cubica solo vas a tomar tres dos y ponerlos afuera y el que sobra queda adentro, espero que ese ejemplo aclare tu otra pregunta.
como saber cual ejemplo usar
acabo de hacer otra vez el ejercicio 6 con el ejemplo 4 y ahora si pude obtener el mismo resultado q usted, pero como saber cual ejemplo usar, xq la primera vez lo hice con el ejemplo 1 y me dio otro resultado completamente distinto
Duda
Hola maestra luz no encuentro donde dijo que podíamos leer como revista
es una que son infantiles primero y otras mas, me podría deci nuevamente please.!!!
Revistas de ciencias
Hola, perdón, acabo de leer tu mensaje pero creo que ya me preguntaste en clase 😀 aquí esta el enlace de todos modos 😉
La numero 5y6
La numero 5 o la seis no las entiendo bien seria tan amable de explicarla para poder entenderla..? y le doy las gracias por este sitio que me esta ayudando mucho gracias por su ayuda
Hola Hipolito, incluí una
Hola Hipolito, incluí una imagen donde se muestran los pasos si los resuelves a mano, si lo haces con la calculadora la respuesta te la da con enteros y decimales. Si acaso se te dificulta, revisa el tema previo que es simplificación de radicales.
[[{«type»:»media»,»view_mode»:»media_large»,»fid»:»1471″,»attributes»:{«class»:»media-image»,»id»:»2″,»typeof»:»foaf:Image»}}]]
5y6
Muchas gracias por su ayuda,entendi perfectamente.Nunca ha estado tan facil pasar el G.E.D.como lo esta ahora,gracias a este Website,,de verdad muchas gracias.
Me da gusto!!
Me alegra saberlo Hipolito, saludos!!!
No entiendo?
Maestra en el problema num 2 no me sale. Favor de explicarme Los pasos….
Pasos
[[{«type»:»media»,»view_mode»:»media_large»,»fid»:»1529″,»attributes»:{«class»:»media-image»,»id»:»2″,»typeof»:»foaf:Image»}}]]
Gracias
Maestra gracias x tomarse el tiempo en mostrarme Los pasos. Ya solo me falta el test d math pero q Cree ahora tambien tengo k hacer el civics test para k me den el GED. Es Una ley nueva en Wi. Uff
Civics Test
Hola Lidiara, no te preocupes ese mismo requerimiento lo tienen en IL, el examen no es difícil. Si acaso es el mismo formato que en IL, va a ser de opción multiple, acá es gratuito y lo puedes repetir las veces que quieras. En este enlace se cubren los temas de la constitucion (civics) http://luzgarfias.com/es/luz/ solo te haría falta ver si se incluyen preguntas sobre la constitución de tu Wisconsin. Saludos!!
Eres la estrella ⭐ que le da energía solar a mi calculadora 😍
Ah que amable, saludos Eustaqui 😉