Buscar la recta de una ecuación
Una ecuación puede tener una o más variables, en específico las ecuaciones que usamos en una grafica tienen dos variables, esto se debe por las coordenadas que hay en el plano cartesiano “x” y “y”. En la siguiente ecuación y = 4x -3 tenemos las dos variables (letras) para resolverla, es necesario asignar un valor a cualquiera de las dos variables.
Las ecuaciones que forman una linea recta en la grafica recibe el nombre de ecuación lineal y para poder marcarla en el plano cartesiano es necesario conocer por lo menos dos puntos. Para eso hay que seguir los siguientes pasos:
(Al final un video y ejercicios)
PASO I
Para identificar el primer punto, hay que asignar un valor a la “x” y asi obtendremos un valor especifico para la “y”, generalmente se usa el cero “0” o números sucesivos. Una vez sustituido el valor de la “x” hay que despejar la “y”
y = 4x – 3
y = 4(0) – 3
y = – 3
Si el valor que le asignamos a la «x» fue 0 y el valor de “y” es -3, las coordenadas del punto A (0, -3). El primer número siempre representa las “x”.
PASO II
Hay que identificar el otro punto para la grafica se pueden asignar otro valor x= 1, se sustituye el valor de «x» en la ecuacion y = 4x – 3
y =4(1) – 3
y= 4 – 3
y = 1
Las coordenadas del punto H (1, 1) y se pueden ubicar en la recta
PASO III
Por último, graficamos la línea en el plano cartesiano usando las coordenadas del punto A y H. Para confirmar que la respuesta es correcta, se pueden asignar otros valores a la “x” y las coordenadas que se obtengan tendrán un orden sucesivo en la recta.
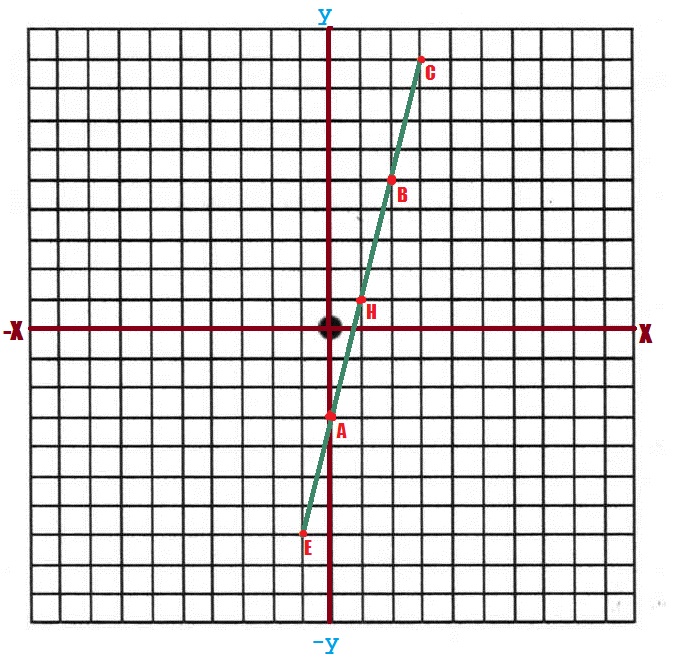
Se asigna otro valor a la “x” en este caso vamos a usar el 2.
y = 4(2) – 3
y = 8-3
y = 5
Las coordenadas del punto B (2, 5)
Como puedes ver ya usamos los valores 0, 1 y 2, ahora veamos que coordenadas nos da si sustituimos la x por los valores 3 y en otra ecuación por -1
y = 4(3) -3
y = 12 -3
y = 9
Las coordenadas del punto C (3,9)
La siguiente si x = -1
y = 4 (-1) – 3
y = – 4 – 3
y = -7
Las coordenadas del punto E (-1, -7)
También pueden resolver las ecuaciones lineales usando la calculadora TI-30XS Multiview.
EJERCICIOS DE PRACTICA
Grafica las siguientes ecuaciones. (La respuesta puede variar de acuerdo al valor que se le de a la “x”)
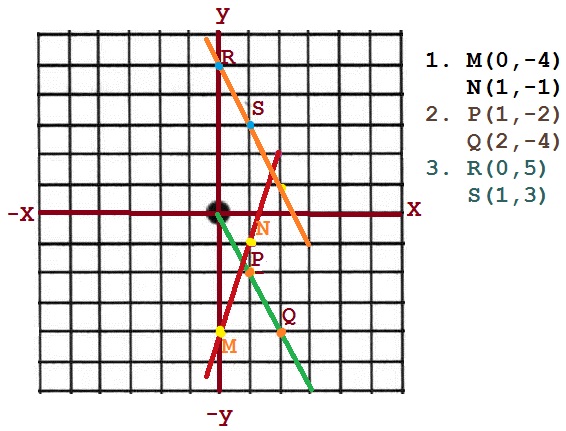
1) y = 3x – 4 2) -2y = 4x 3) 2x + y = 5
RESPUESTA
1. y = 3x – 4 Si x = 0
y = 3 (0) – 4
y = 0 – 4
y = 4 las coordenadas serian M (0, -4)
y = 3x – 4 Si x = 1
y = 3 (1) – 4
y = 3 – 4
y = -1 las coordenadas serian N (1, -1)
2. –2y = 4x Si x = 1
-2y = 4(1)
-2y = 4
y = 4/-2
y = -2 las coordenadas del P (1, -2)
-2y = 4x Si x = 2
-2y = 4(2)
-2y = 8
y = 8/- 2
y = – 4 las coordenadas del punto Q (2, -4)
3. 2x + y = 5 Si x = 0
2 (0) + y = 5
y = 5 las coordenadas serian R (0, 5)
2x + y = 5 Si x = 1
2(1) + y = 5
2+ y = 5
y = 5 – 2
y = 3 las coordenadas serian S (1, 3)