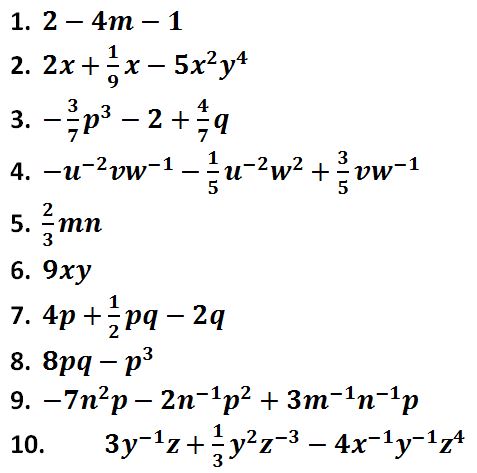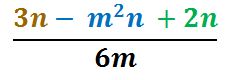
División de polinomio con monomio

por Luz | Abr 18, 2015 | Algebra, Matematicas

Una vez que te has familiarizado con la división de términos se te va a facilitar las diferentes variables de división que se presentan en algebra. Primero vamos a recordar lo siguiente:

• Un monomio se compone de un término sin importar el número de incógnitas o letras que tenga (-4x³yz⁴). 
• Un binomio se compone de dos términos y un trinomio de tres, estos también se conocen como polinomios que son los que ya tienen dos o más  términos, por ejemplo: binomio (5m^-3n² – 8mn) , trinomio (-3xy + xy – 2x²y).
• Cuando tenemos más de tres términos es más común que los llamen polinomio (7mn⁴ -3m² +mn² +2mn).

Ahora veamos como dividir un polinomio (que puede tener dos o más términos) con un monomio, quiere decir que en la parte del numerador vamos a tener varios términos y en la parte del denominador tendremos solo uno.

EJEMPLO I

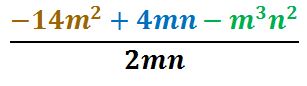
PASO I 

Dividir, siguiendo los pasos de la división, el primer término que está en café.

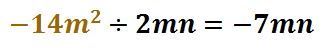
PASO II 

Dividir el segundo término  (azúl) con el denominador.

PASO III 

Dividir el tercer término (verde) con el denominador.

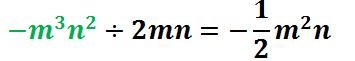
PASO IV 

Representar tu respuesta juntando cada una de las anteriores

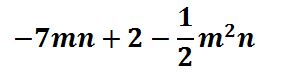
EJEMPLO II

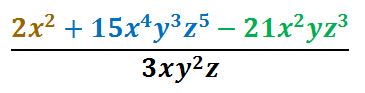
PASO I  

Dividir, siguiendo los pasos de la división, el primer término que está en café.

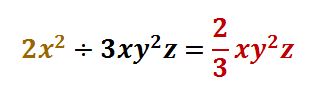
PASO II  

Dividir el segundo término  (azúl) con el denominador.

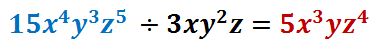
PASO III  

Dividir el tercer término (verde) con el denominador.

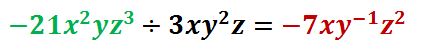
PASO IV   

Representar la respuesta

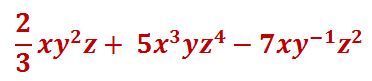
EJEMPLO III

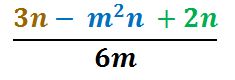
PASO I 

Dividir, siguiendo los pasos de la división, el primer término que está en café. Si se te dificulta visita “Fracciones”.

Al dividir 3n ÷ 6m = ½mn

Al dividir enteros solo escribe el número uno en lugar del denominador y se multiplica cruzado. 

PASO II 

Dividir el segundo término  (azúl) con el denominador.

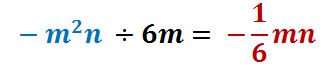
Recuerda que si no hay coeficiente o número este va a ser 1 y al dividir 1entre 6 nos da un sexto.

PASO III 

Dividir el tercer término (verde) con el denominador

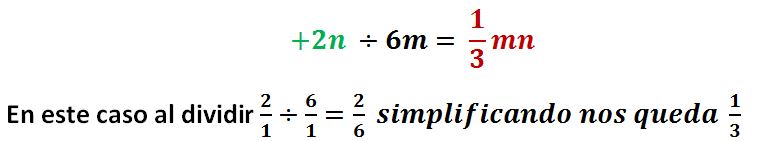
PASO IV 

Representar la respuesta

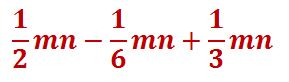
PASO V

Simplificar términos semejantes, este paso no siempre va a ser necesario, solo cuando hay términos semejantes que son aquellos que tienen la misma incógnita o letra y el mismo exponente. En el ejemplo anterior todos son términos semejantes y se simplifican aplicando la ley para suma y resta. Aquí se puede repasar la suma y resta de fracciones y recuerda que para algunos exámenes puedes usar la calculadora.

EJERCICIOS DE PRÁCTICA

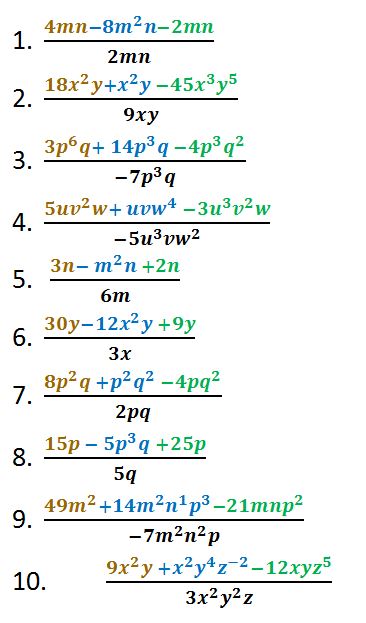
RESPUESTAS