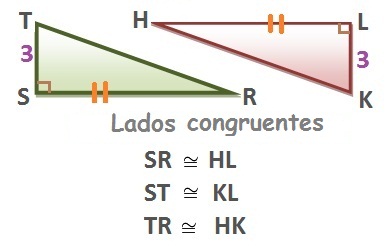
Triángulos semejantes
Los triángulos semejantes tienen la misma forma, diferente tamaño y medidas proporcionales. Un tipo de triángulos semejantes es el triángulo rectángulo y se forma cuando tenemos presente un ángulo de 90 grados (ángulo recto).
Estos triángulos los podemos encontrar en diversas circunstancias de la vida cotidiana como en la sombra de un poste, un edificio, una barda, etc. En este caso tenemos la sombra de un árbol y una persona.
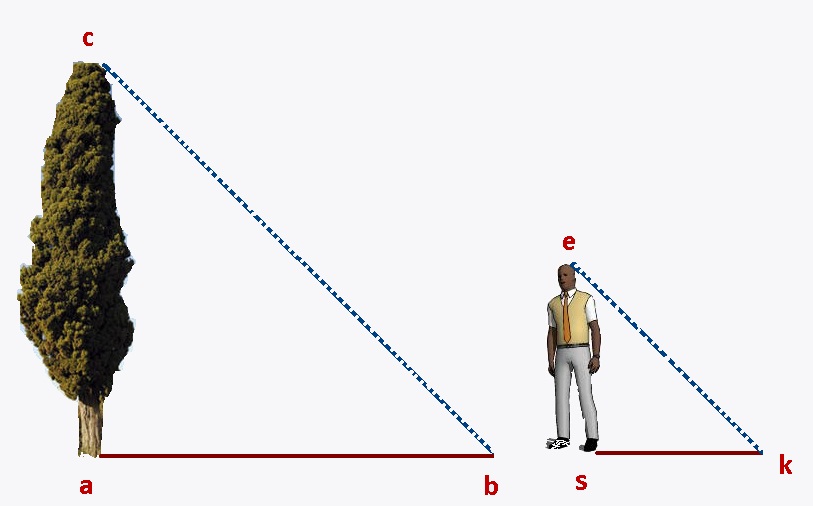
Asignando valores tendríamos
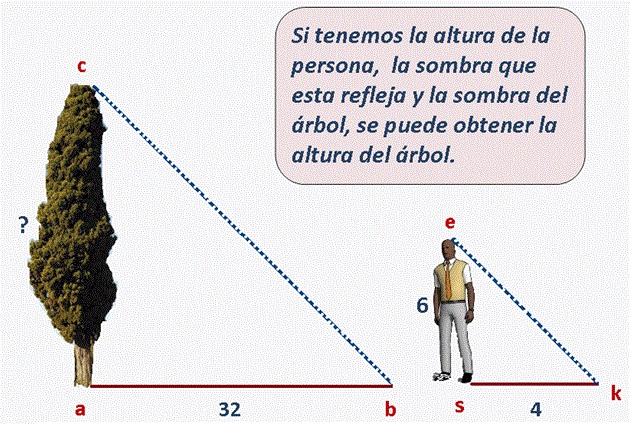
Primer método:
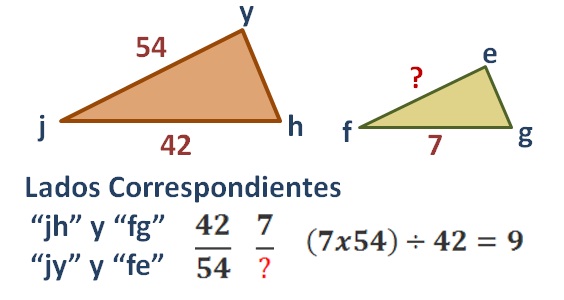
Identificar los lados correspondientes, “ab” y “sk” después dividir la medida del lado más largo (sombra del árbol) con la del lado más chico (sombra de la persona) y multiplicarlo por la altura de la persona.
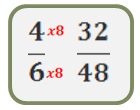
Ahí tendríamos (32 ÷ 4) x 6 = 48.
Segundo método:
Puede ser un poco más compleja para algunos y consiste en ordenar los datos por regla de tres identificando los lados correspondientes y quedaría de la siguiente manera:

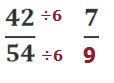
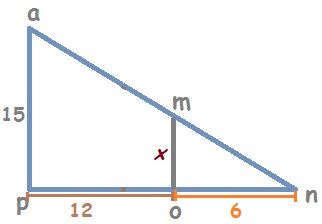
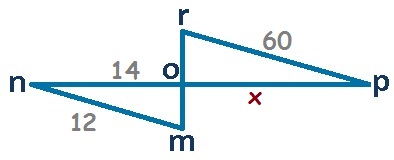
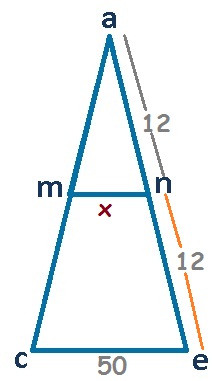
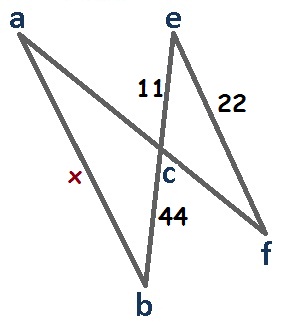
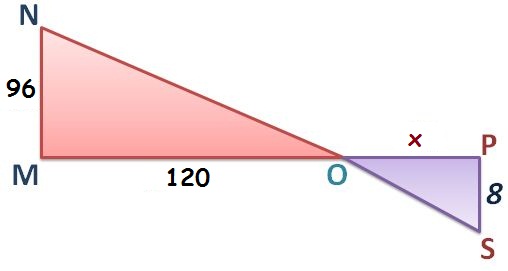
RESPUESTAS
1. 5, 2. 70, 3. 25, 4. 88, 5. 10
