Una función es una relación numérica de valores que tienen una relación de dependencia, quiere decir que si tenemos dos cantidades o valores numéricos el primero va a depender siempre del segundo.  

Un ejemplo sencillo para entender una función son las semanas laborales, si una persona gana $300 durante una semana laboral. Para ganar $600 debe trabajar 2 semanas y así sucesivamente. El ingreso que obtenga siempre va a depender del número de semanas que trabaje. ¡Sencillo, ¿verdad?! 

Ahora, hay una variedad inmensa de funciones, pero ahora nos vamos a enfocar en las cuatro mas comunes, algunas mas complicadas que otras: constante, lineal, cuadratica y cúbica.

FUNCIÓN CONSTANTE

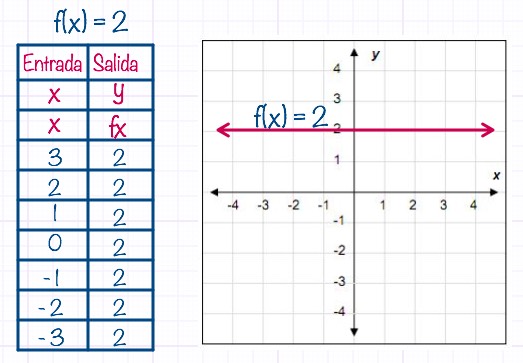
La función es constante cuando permanece siempre igual, sin importar cual sea el valor de entrada.

La fórmula para esta función es fx= c

 

FUNCIÓN LINEAL

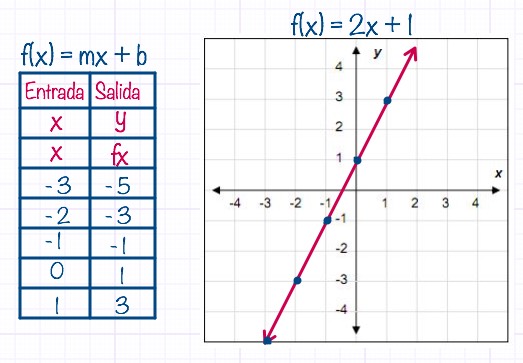
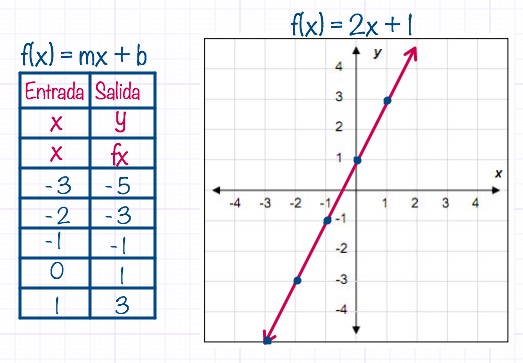
Esta función nos permite dibujar una linea recta y se forma usando la fórmula fx = mx + b donde “m” es la pendiente (inclinación de la recta) y “b” es el intercepto en “y”. Ahora por cada valor que le demos a la “x” vamos a obtener un valor correspondiente para “y” (fx).

Para aprender mas sobre este tema se pueden estudiar los siguientes enlaces.

Pendiente

Obtener la ecuación de una recta

Graficar una ecuación

fx = 2x + 1

fx = 2(1) + 1

fx = 2 + 1

fx = 3

FUNCIÓN  CUADRATICA

fx = ax² + bx + c

La función cuadratica es un polinomio de segundo grado, siempre va a cambiar de dirección en un punto que se llama VÉRTICE. 

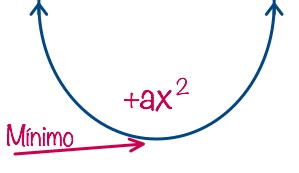
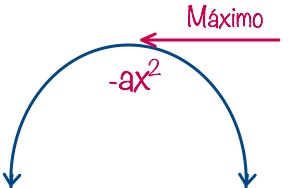
Siempre que el valor de +ax² es positivo, la dirección de la parábola va hacia arriba (como una U). Siempre que el valor de -ax² es negativo, la dirección de la parábola va hacia abajo (como una «U» invertida).

Los puntos claves en una parábola son el vértice, las raíces y el intercepto en «y».

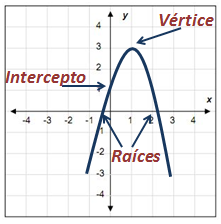
Para aprender a obtener los valores en la parábola visita esta lección.

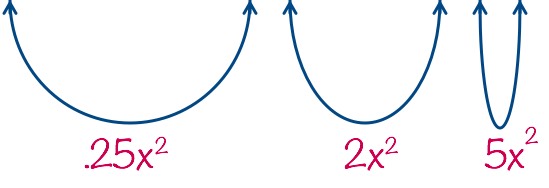
Otra pista importante en las funciones cuadraticas es que mientras mas chico sea el valor de “ax² » mas ancha va a ser la parábola.

FUNCIÓN CÚBICA

f(x)= ax³ + bx² – cx – d

Una función cúbica es un polinomio de tercer grado. Muchos de estos polinomios tienen tres raíces, quiere decir que la grafica va a tener tres puntos que atraviesan «x».

Si la «+ax³» es positiva, la gráfica va a iniciar de abajo hacia arriba (de izquierda a derecha). 

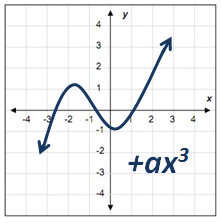
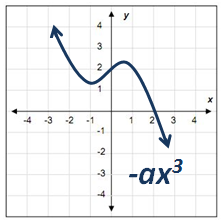
Si la «- ax³« es negativa, la gráfica va a iniciar de arriba hacia abajo (de izquierda a derecha).

Ejemplo:

f(x)= x³ + x² – 4x – 4

0 = x³ + x² – 4x – 4  Se iguala a cero el polinomio. 

0 = (x³ + x²) + (- 4x – 4) Se agrupa en pares.

0 = x² (x +1) – 4 (x + 1)Se factoriza cada factor.

0 =  (x + 1) (x² – 4) Se agrupan (los que quedan fuera del paréntesis forman otro par).

0 =  (x + 1) (x + 2) (x – 2) Se factoriza el  (x² – 4).

x = {- 1, – 2, + 2}  Los tres valores de «x» son los números que quedan de la factorización pero con signo contrario.

Para representar las coordenadas, los valores en «y» siempre van a ser cero. Así tenemos: (-1, 0), (-2, 0) y ( 2, 0)

Otro dato importante es el intercepto en «y» que siempre a a ser el valor de «d», en este caso, el -4 y su coordenada quedaría (0, -4).