Balanceo de ecuaciones químicas
Una de las habilidades que se evalúan cuando se hace un examen de química es el balanceo de ecuaciones. Para eso es importante conocer estar familiarizado con los elementos de la tabla periodica para ello puedes visitar esta liga. Las ecuaciones químicas no son otra cosa que la interacción (mezcla o convinación) entre uno o mas elementos. Al final hay un video donde se explica el tema.
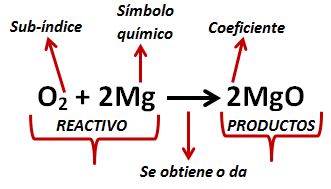
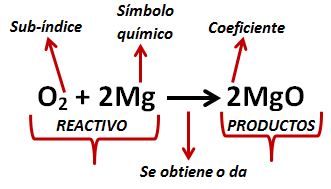
En la parte izquierda de la ecuación tenemos los “reactivos” que son los elementos que se unen para dar el producto, la flecha nos indica lo que se obtiene al combinar dichos elementos.
En la ecuación, las letras indican los símbolos químicos, estos se pueden representar con una letra mayúscula, o con una mayúscula y minúscula juntas.
El número pequeño en la parte inferior derecha de cada símbolo químico es el sub-índice y nos indica el número de átomos, de ese elemento, que intervienen en la ecuación.
El número grande es el coeficiente y nos indica la cantidad de moléculas que se forman con los elementos.
Balancear una ecuación quiere decir que debemos tener la misma cantidad de átomos en ambos lados de la fecha, en otras palabras, lo mismo que esta a la izquierda debe estar a la derecha, aunque sea en diferente orden.
Para contar los átomos se toma en cuenta el sub-índice y el coeficiente de cada elemento.
Ejemplos:
2H2 Aquí tenemos 2 átomos de hidrogeno, lo obtenemos multiplicando el coeficiente por el sub-índice.
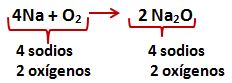
Cuando el coeficiente esta al inicio cuenta para todos los símbolos químicos que están al frente de él. Contando tenemos 4 átomos de sodio (Na) y dos de oxigeno (O)
Una vez que aprendes a identificar la cantidad de átomos, puedes balancear ecuaciones y en la Tabla Periódica vas a encontrar el nombre y la abreviación de cada elemento.
Ejemplo I
El sodio (Na) reacciona con el oxígeno (O) y produce oxido de sodio 
PASO I Identifica la cantidad de átomos que intervienen en los reactantes (izquierda) que tenemos.
4 Sodios
2 Oxígenos
PASO II Identifica la cantidad de átomos que se producen
2 sodios
1 oxígenos
PASO III Determinar si la ecuación esta balanceada o no. Es este caso no porque nos faltan dos sodios y un oxígeno.
PASO IV Modificar la ecuación para que quede balanceada. Para tener 4 sodios (Na) incluimos un coeficiente, en este caso el 2.
PASO IV Por ultimo confirma que la ecuación este balanceada
Ejemplo II
En esta ecuación tenemos el metano 
que es un gas y reacciona en contacto con el oxígeno (O) y una chispa. De esta reacción se produce agua 
y dióxido de carbono 
PASO I Identifica la cantidad de átomo que se tienen en los reactantes (parte izquierda de la flecha)
1 carbono
4 hidrógenos
2 oxígenos
PASO II Identifica la cantidad de átomos que se producen (parte derecha de la flecha).
1 carbono
2 hidrógenos
3 oxígenos
PASO III Determinar cuántos átomos de cada elementos nos hacen falta y analiza que coeficientes agregarías para balancear la ecuación.
Primero ¿qué coeficiente tendrías que agregar para que en la molécula del agua 
haya 4 hidrógenos? Una vez que agregues los hidrógenos balancea nuevamente la ecuación y determina que cantidad de átomos de oxigeno te hacen falta en el lado izquierdo de la flecha y escribe el coeficiente correspondiente.
Observa como los 4 oxígenos están distribuidos 2 en la molécula del agua y 2 en el dióxido de carbono.
Al balancear una ecuación es posible que tengas que hacer cambio tanto en los reactantes y en los productos.
EJERCICIOS DE PRACTICA
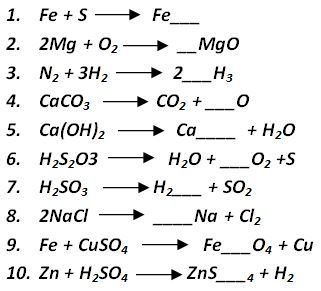
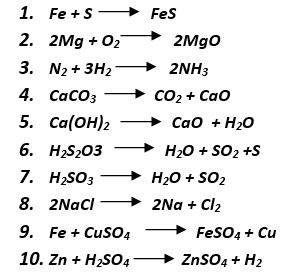
Identifica la cantidad de átomos que se encuentran en los reactantes (parte izquierda de la ecuación) y determina que cambio debes hacer en los productos (parte derecha). Si no conoces el elemento que representa cada simbolo quimico, revisa la Tabla Periódica.
RESPUESTAS
Entre GED, HiSET o TASC, ¿cuál examen debo hacer?
Estrategias para el examen de estudios sociales
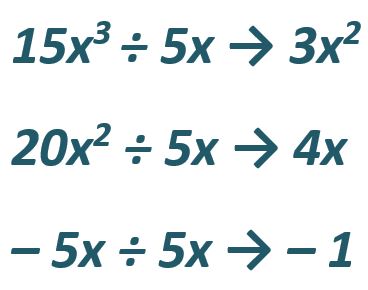
Factorizar polinomios
Un monomio está compuesto por un solo término el cual incluye signo, coeficiente, incógnita y exponente por tanto un polinomio es aquel que tiene dos o más términos. Para factorizar un polinomio vamos a seguir los siguientes pasos:
Si tienes dificultad con estos temas es recomendabel revisar primero:
Ejemplo I
b2 + 3b
PASO I: Buscar el factor común de ambos términos. El factor común para las incógnitas (letras) es la que se encuentra en ambos términos. Para entender el factor común de los coeficientes (números) revisa este enlace.
Para este caso el factor común es la “b”
PASO II: Dividir cada termino entre el factor común que se encontró, ósea que vamos a dividir b2 ÷ b y 3b ÷ b. Si tienes dificultad para dividir términos, revisa este enlace.
b2 ÷ b = b
2b ÷ b = 2
PASO III: Se escriben las respuestas dentro de un paréntesis incluyendo los signos, y afuera del paréntesis se escribe el factor común.
b (b + 2)
Ejemplo II
10n – 30mn2
PASO I: Buscamos el factor común para las incógnitas (letras) y los coeficientes (números)
10 → 2, 5, 10
30 → 3, 10
n – mn2 → n
Nuestro factor común va a ser el 10 porque se repite en ambos coeficientes y la n
OJO: Si al factorizar se repite más de dos veces un número escogemos el MAYOR como factor común
PASO II: Dividimos los términos entre los factores comunes
10n ÷ 10n = 1
– 30mn2 ÷ 10n = – 3mn
PASO III: Poner las respuestas que obtuvimos de las divisiones dentro de un paréntesis respetando signos y afuera el factor común que obtuvimos
10n(1 – 3mn)
Ejemplo III
15x3 + 20x2 – 5x
PASO I: Obtenemos el factor común de los coeficientes y las incógnitas
15 → 3, 5
20 → 2, 4, 5, 10
5 → 1, 5
Factor común → 5
Para las incógnitas es x
PASO II: Dividimos cada termino entre el factor común
15x3 ÷ 5x → 3x2
20x2 ÷ 5x → 4x
– 5x ÷ 5x → -1
PASO III: Escribimos las respuestas de la división dentro de un paréntesis incluyendo los signos y afuera el factor común.
5x (3x2 + 4x – 1)
Ejercicios de práctica
- 8x2 + 12xy
- m2 + m
- p3 – p5 – p7
- 35x2y3 – 70x3
- xy – yz
- 5c2 + 15c3
- 2b2c + 6bc2
- 4m2 – 8m + 2
Respuestas
- 4x(2x + 3n)
- m (m+1)
- x3 (1 + x2 – x4)
- 35x2(y3 – 2x )
- y(x –z)
- 5c2(1 + 3c)
- 2bc(b + 3c)
- 2(2m2 – 4m + 1)