De la factorización de trinomios, el de cuadrados perfectos es uno de los más fáciles ya que solo tenemos que entender el concepto de la raíz cuadrada perfecta, que no es otra cosa que buscar el número que multiplicado por el mismo nos de el valor que buscamos, por ejemplo la raíz cuadrada de 25 es 5 porque 5 por 5 es 25 y así sucesivamente, este tema lo puedes revisar el siguiente video.
Al buscar los factores de un trinomio cuadrado perfecto se van a obtener aquellos que multiplicados por sí mismo nos dan el trinomio. Si ya sabes multiplicar factores se te va a facilitar entender este tema, veamos el primer ejemplo y los pasos para resolverlo:
Antes de aplicar este método de factorización debes determinar si el primer y tercer término del trinomio son cuadrados perfectos, en el caso de las incógnitas o letras, solo es ver si su exponente es par, quiere decir que la raíz cuadrada de x4 = x2, de m6n2 = m3n y así sucesivamente.
x2 + 6x + 9
PASO I
Obtener la raíz del primer término (azúl), abrir un paréntesis y poner la respuesta. (Para obtener la raíz cuadrada de cualquier incognita, simplemente se divide el exponente entre 2).
(x
PASO II
Identificar el signo de segundo término (verde) y escribirlo enseguida.
(x +
PASO III
Obtener la raíz cuadrada del tercer término (rojo), escribelo después del signo y cerrar el paréntesis.
(x + 3)
PASO IV
Elevar al cuadrado la respuesta.
(x + 3)2
Ejemplo II
x4 + 4x2y + 4y2
PASO I
Obtener la raíz cuadrada del primero y tercer término – azul y rojo- (recuerda que los exponentes de las incógnitas se dividen entre dos).
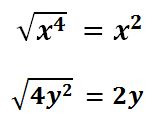
PASO II
Escribir las respuestas dentro de un paréntesis.
(x2 2y)
PASO III
Escribir el signo del segundo término y elevas al cuadrado.
(x2 + 2y)2
Para comprobar la respuesta, simplemente se multiplica el binomio por el mismo.
(x2 + 2y) (x2 + 2y)
x4 + 4x2y + 4y2
Ejercicios de practica
- 4 – 4x + x2
- 4x2 + 12x + 9
- x2y2 + 8xy +16
- 25m2 – 10mn + n2
- m2n2 + 10mn + 25
- 36x2 – 108x + 81
- 9m2 + 12mn + 4n2
- m2 + 4mn + 4n2
- 9x4 – 30x3y + 25x2y2
- 16m8 – 64m5n – 64m2n2
RESPUESTAS
Las respuestas las puedes representar (x – 2)2 o (x – 2) (x – 2)
- (x – 2)2
- (2x + 3)2
- (xy + 4)2
- (5m – n)2
- (mn + 5)2
- (6x – 9)2
- (3m + 2n)2
- (m + 2n)2
- (3x2 – 5xy)2
- (4m4 – 8mn)2
Pasos para resolverlos
1. x2– 4x + 4 Primero verifica que el trinomio este ordenado
- (x ) (x ) Obten la raíz del primer término – separando las x
- (x 2) (x 2) Obten la raíz del tercer término – √4 = 2
- (x – 2) (x 2) En el primer factor escribes el signo del segundo término.
- (x – 2) (x – 2) Multiplicas el singo del primer término por el signo del tercero. – por + = –
2. 4x2 + 12x + 9
- (2x ) (2x ) Obten la raíz del primer término – √4 = 2 y √x2 = x
- (2x 3) (2x 3) Obten la raíz del tercer término – √9 = 3
- (2x + 3) (2x 3) En el primer factor escribes el signo del segundo término.
- (2x + 3) (2x + 3) Multiplicas el singo del primer término por el signo del tercero. + por + = +
3. x2y2 + 8xy +16
- (xy ) (xy ) Obten la raíz del primer término – √x2 = x y √y2 = y
- (xy 4) (xy 4) Obten la raíz del tercer término – √16 = 4
- (xy + 4) (xy 4) En el primer factor escribes el signo del segundo término.
- (xy + 4) (xy + 4) Multiplicas el singo del primer término por el signo del tercero. + por + = +
4. 25m2 – 10mn + n2
- (5m ) (5m ) Obten la raíz del primer término – √25 = 5 y √m2 = m
- (5m n) (5m n) Obten la raíz del tercer término – √n2 = n
- (5m – n) (5m n) En el primer factor escribes el signo del segundo término.
- (5m – n) (5m – n) Multiplicas el singo del primer término por el signo del tercero. – por + = –
5. m2n2 + 10mn + 25
- (mn ) (mn ) Obten la raíz del primer término – √m2 = m y √n2 = n
- (mn 5) (mn 5) Obten la raíz del tercer término – √25 = 5
- (mn + 5) (mn 5) En el primer factor escribes el signo del segundo término.
- (mn + 5) (mn + 5) Multiplicas el singo del primer término por el signo del tercero. + por + = +
6. 36x2 – 108x + 81
- (6x ) (6x ) Obten la raíz del primer término – √36 = 6 y √x2 = x
- (6x 9) (6x 9) Obten la raíz del tercer término – √81 = 9
- (6x – 9) (6x 9) En el primer factor escribes el signo del segundo término.
- (6x – 9) (6x – 9) Multiplicas el singo del primer término por el signo del tercero. – por + = –
7. 9m2 + 12mn + 4n2
- (3m ) (3m ) Obten la raíz del primer término – √9 = 3 y √m2 = m
- (3m 2n) (3m 2n) Obten la raíz del tercer término – √4 = 2 y √n2 = n
- (3m + 2n) (3m 2n) En el primer factor escribes el signo del segundo término.
- (3m + 2n) (3m + 2n) Multiplicas el singo del primer término por el signo del tercero. + por + = +
8. m2 + 4mn + 4n2
- (m ) (m ) Obten la raíz del primer término – √m2 = m
- (m 2n) (m 2n) Obten la raíz del tercer término – √4 = 2 y √n2 = n
- (m + 2n) (m 2n) En el primer factor escribes el signo del segundo término.
- (m + 2n) (m + 2n) Multiplicas el singo del primer término por el signo del tercero. + por + = +
9. 9x4 – 30x3y + 25x2y2
- (3x2 ) (3x2 ) Obten la raíz del primer término – √9 = 3 y √x4 = x2
- (3x2 5xy) (3x2 5xy) Obten la raíz del tercer término – √25 = 5 , √x2 = x y √y2 = y
- (3x2 – 5xy) (3x2 5xy) En el primer factor escribes el signo del segundo término.
- (3x2 – 5xy) (3x2 – 5xy) Multiplicas el singo del primer término por el signo del tercero. – por + = –
10. 16m8 – 64m5n – 64m2n2
- (4m4 ) (4m4 ) Obten la raíz del primer término – √16 = 4 y √m8 = m4
- (4m4 8mn) (4m4 8mn) Obten la raíz del tercer término – √64 = 8, √m2 = m y √n2 = n
- (4m4 – 8mn) (4m4 8mn) En el primer factor escribes el signo del segundo término.
- (4m4 – 8mn) (4m4 – 8mn) Multiplicas el singo del primer término por el signo del tercero. – por – = –

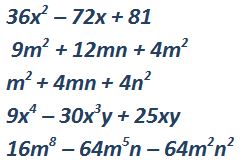
Duda
Podrian explicar alguien como hicieron para resolver los ejercicio n°7 y 10
Raíz cuadrada
Solo obtienes la raíz cuadrada de el número y después el de la letra. Si puedes revisa antes las raices cuadradas exactas. Para obtener la raíz cuadrada de las literales (letras) simplemente divides entre dos su exponente.
9m2 + 12mn + 4m2 – En este caso, raíz cuadrada de 9 = 3, de m2 es «m». Raíz cuadrada de 4 es 2 y de m2 es «m»
16m8 – 64m5n – 64m2n2 – En este haces los mismo, obtén la raíz cuadrada de 16, de m8 que sería m4, de 64=8 y me m2 es «m», de n2 es «n»
sacas la raiz de el primer termino y el ultimo por ejemplo x cuadrada mas 2 mas 1 seria
(x-1) al cuadrado por que el primer y ultimo termino multiplicados te deben
de dar el segundo termino ósea 1 que es lo que vale Xpor1 y luego el resultado de eso por 2 y así es como se resuelve
Así es Fabio, lo básico es identificar si el primer y tercer término tienen raíz cruadrada y solo en esos casos se aplica este método. Para los que no entran en esta categoría se usan otros métodos.
Estas confundido porque en el ejercicio No. 7 hay un error, ya que el tercer termino debería ser 4n2 (cuatro «n» al cuadrado) y no cuatro «m» al cuadrado, como esta escrito.
Gracias por el comentario María, voy a revisarlo. ¡Saludos!
la respuesta de la número 6 no corresponde , es otro tipo de factorización . sería 9(4x²-8x+9)
Gracias por el comentario Gianina, ya la edite.
Duda: Problema 6.
Muchas graciaspor la explicacion esta muy buena! Sin embargo me parece que el trinomio del ejercicio numero 6 no es un trinomio cuadrado perfecto por lo que especifican las reglas, Si estoy mal por favor corregidme de otra forma agradeceria una correccion en el post para que cualquier otro usuario pueda verificar correctamente. Muchas gracias por todo!
Trinomio cuadrado perfecto
Si es un trinomio cuadrado perfecto, pero tienes razón, en la explicación hace falta especificar que el valor del primer termino de las x2 también debe ser una raíz cuadrada exacta para que aplique la regla. En este caso la raíz cuadrada de 36 es 6; x2 es x y del 81 es 9.
Errores
Los ejercicios 6, 7, 9 y 10 no son trinomios cuadrados perfectos, por ende las respuestas están malas, por favor corregirlo.
por favor corregirlo? eeeee no de hecho esta bastante bien hecho.
🙂 😉 Gracias por tu comentario
felicitaciones por saber matemáticas y explican muy bien de eso es que me apoyo para estudiar para las evaluaciones.
Gracias por tu comentario Mariana, me alegra que te ayuden estos recursos. ¡Saludos!!
Saludos Mariana, gracias por tu comentario 🙂
No entendi
Aquí hay otros temas de factorización, espero te ayuden. https://www.spanishged365.com/?s=factorizar
No entendi
¿Hay una pregunta en especifico que quieras aclarar?
sorry I didn’t understand you could give me private lessons
Hola, si hablas el español, hay unas clases en linea que he estado impartiendo en el canal de YouTube los lunes a las 8:00 pm hora este.
muy útil la info. gracias :3
Un gusto Isaac, ¡saludos! 😉
gracias por la informacion la necesitaba mañana tengo examen de matematicas un gusto y muchas gracias
Jose, espero que te haya ido bien en el examen, hasta ahora estoy viendo varios comentarios pasados. Te mando saludos.
Pueden poner el procedimiento de todos los ejercicios de practica?
Por favor.
Se los agradecería mucho. ♥♥♥
Si pusieran el procedimiento que se hace para hacer cada una de los ejercicios de practica por separado.♥
Si Daniel voy a hacer un video con los procedimientos o en todo caso las soluciones paso a paso. Gracias por la recomentación, ¡saludos!
Buenas una pregunta es que me pusieron una tarea con referencia a los ejercicios de la imagen que esta al comienzo y no logro resorlverlos ayuda…
Las respuestas y los pasos están al final, equivalen a los ejercicios del 6 al 10.