Guía para el examen de matemáticas

Área I, un 25% incluye solucionar problemas cuantitativos con números racionales (fracciones)

• Colocar en orden fracciones y decimales, poder identificarlos en la recta numérica.

• Aplicar propiedades numéricas (conmutativa, asociativa, identidad de la suma, inverso aditivo, distributiva) que implican múltiplos y factores.

• Simplificar expresiones numéricas con exponentes racionales (fracciones).

• Identificar el valor absoluto de un número racional en términos de su distancia del 0 en la recta numérica y determinar la distancia entre dos números racionales en la recta numérica.

• Hacer cálculos con números racionales y resolver problemas con números racionales (fracciones).

• Escribir y hacer cómputos con expresiones numéricas con cuadrados y raíces cuadradas, cubos y raíces cubicas de números racionales positivos

• Determinar cuándo una expresión numérica es indefinida.

• Calcular tasas unitarias.

• Usar factores de escala para calcular la magnitud de un cambio de tamaño y convertir de dibujos reales a dibujos a escala.
• Resolver problemas aritméticos con dos pasos del mundo  real que  implican índices, proporciones y porcentajes.

Área II, un 20% incluye la solución de problemas cuantitativos en medidas

• Calcular el área y el perímetro de varias formas: triángulos, rectángulos, polígonos y figuras compuestas

• Encontrar las longitudes de los lados de triángulos, rectángulos y polígonos cuando se da el área o el perímetro (despejar formulas).

• Calcular el área y la circunferencia de círculos y encontrar el radio o el diámetro cuando se da el área o la circunferencia.

• Usar el teorema de Pitágoras (a² + b² = c²) para determinar las longitudes desconocidas de los lados de un triangulo recto o  buscar el valor de la hipotenusa.

• Calcular el volumen y el área de superficie de prismas y pirámides rectangulares, cilindros, conos, esferas y figuras compuestas.

• Resolver la altura, el radio, el diámetro o las longitudes de los lados de cilindros, conos, y pirámides rectangulares cuando se da el volumen o área de superficie.

• Representar, desplegar e interpretar datos categóricos en graficas de barra, graficas de circulo, grafica de puntos, histogramas, diagramas de caja, tablas y diagramas de dispersión.

• Calcular la media, mediana, moda, rango y promedio ponderado; calcular el valor de un dato faltante cuando se proveen el promedio o los demás valores.

• Usar técnicas de conteo para resolver problemas y encontrar combinaciones y permutaciones.
• Determinar la probabilidad de eventos simples y compuestos.

Área III, un 30% incluye la solución de problemas algebraicos con expresiones y ecuaciones

• Calcular expresiones lineales.

• Evaluar expresiones lineales, polinomios y racionales.

• Crear ecuaciones cuadráticas y expresiones lineales, ecuaciones y desigualdades con las descripciones escritas que se ofrezcan.

• Calcular y factorizar con polinomios.

• Calcular expresiones racionales.

• Crear expresiones racionales con las descripciones escritas que se ofrezcan.

• Resolver problemas algebraicos y de la vida real que implican ecuaciones lineales.

• Resolver problemas algebraicos  y de la vida real que implican un sistema de dos ecuaciones lineales.

• Resolver problemas aritméticos y de la vida real con desigualdades y trazar graficas de las soluciones en una recta numérica.
• Resolver ecuaciones cuadráticas en una variable.

Área IV, un 25% incluye solución de problemas algebraicos con gráficas y funciones

• Ubicar puntos y trazar graficas de ecuaciones lineales en el plano de coordenadas.

• Encontrar la pendiente de una línea de una gráfica, ecuación o tabla.

• Entender que una tasa unitaria es equivalente a una pendiente en una relación proporcional.

• Para una relación lineal o no lineal, trazar gráficas e interpretar las características clave de graficas y tablas en términos de cantidades.

• Escribir la ecuación de una línea con una pendiente dada a través de un punto dado.

• Escribir la ecuación de una línea con una pendiente dada a través de un punto dado.

• Escribir la ecuación de una línea que atraviesa dos puntos específicos dados.

• Usar la pendiente para identificar líneas paralelas y perpendiculares, y para resolver problemas geométricos.

• Comparar dos relaciones proporcionales distintas o dos funciones lineales o cuadráticas cuando cada una de ellas se representa de manera distintas

• Usando una tabla o gráfica, representar o identificar que una función tiene exactamente  un egreso por cada ingreso
• Evaluar funciones lineales y cuadráticas.

     Las nuevas preguntas del examen de matemáticas varían en formato, en algunas hay que elaborar las gráficas, escribir la respuesta e incluye preguntas con problemas verbales, las siguientes preguntas sirven de practica pero para familiarizarse con el formato de las nuevas preguntas visitar: Nuevo examen

    Todos las preguntas presentadas a continuación son temas que también se incluyen en el examen.

1. Marcos trabajo 30 horas esta semana y gano a  $7.50 por hora. Su amigo Andrés gano a $9.00 por hora.  ¿Cuántas horas debió trabajar Andrés para igualar el ingreso de Marcos en 30 horas?

a) 30

b) 25

c) 28

d) 20

e) 27

2. Laura quiere saber cuánto representan en °F,  22 °C; si utiliza la siguiente formula, ¿qué resultado obtendrá redondeado a la unidad mas proxima?

a) 60 °F  

b) 58 °F  

c) 65 °F  

d) 72 °F  

e) 75 °F  

3. Carlos llena su tanque con 32 galones, si le queda ¼ de tanque, ¿cuántos galones ha usado?

a) 8

b) 16

c) 30

d) 28

e) 24

4. Leticia tiene un terreno que mide 49cm cuadrados, ¿cuánto mide cada lado del terreno si forma un cuadrado perfecto?

a) 12.25

b) 7

c) 24.5

d) 7.5

e) 8

5. Obtén el área de la siguiente figura

6. Si Armando tiene un trozo de madera que mide 8 pies, ¿cuántos trozos de 3 pulgadas puede obtener? (1 pie = 12 pulgadas) 

a) 90

b) 28

c) 30

d) 32

e) 25

7. El matrimonio Martínez quiere poner una pequeña albarca en su patio, si quieren que mida 6 metros de diámetro y 1.5 metros de profundidad, ¿Cual es el volumen total de la alberca?

a) 10.59

b) 4.5

c) 28.26

d) 42.39

e) 4.71

8. ¿Cuál es el interés ganado con un capital de $7,000.00 al 14% anual en 15 meses?

a) $1,200.00

b) $980.00

c) 1,225.00

d) $245.00

e) $2,940.00

9. Si Melisa usa 3 tazas de harina para preparar 2 tartas, ¿cuántas tazas necesitara para preparar 5 tartas?

a) 6 ¼   

b) 5

c) 7

d) 9

e) 7 ½ 

10. Un poste de 25 pies forma una sombra de 15 pies de largo a cierta hora del día. Si  quieren poner un cable de tensión que baya de la punta del poste al extremo donde termina la sombra, ¿cuánto debe medir el cable de tensión? Redondea tu respuesta a la unidad más cercana.

a) 39 pies

b) 29 pies

c) 33 pies

d) 25 pies

e) 35 pies

11. En un triangulo rectángulo el ángulo “a” mide (3x-15) y el ángulo  “c” mide (x+25).  ¿Cuál es la medida del ángulo “a”?

a) 20

b) 80

c) 45

d) 60

e) 65

12. Julia tiene 40 pies de tela para diseñar una cortinas, si cada cortina va a medir 2 pies con 6 pulgadas. ¿Cuántas cortinas puede hacer?

a) 12

b) 18

c) 6

d) 16

e) 18

13. Estefania necesita 8 segmentos de tela para hacer unas servilletas, si quiere que cada servilletero mida 1 pie con 9 pulgadas. ¿Qué cantidad de tela necesita? Representa tu respuesta en pies.

a) 22

b) 21

c) 14

d) 15

e) 12

14. Evalué 

a) -16

b) 2

c) 16

d) 12

e) -2

15. Evalué

a) 649

b) 625

c) 607

d) 36

e) 663

16. La medida de los ángulos de un triangulo tiene una razón de 3:2:1. ¿Con cuál expresión se puede obtener la medida del ángulo menor?

a) 6 = 180

b) x + 2x + 2x = 180

c) 180 = 3x + 2x + 2x

d) x = 180/6

e) 3:2:1= 180

17. En un determinado momento del día, una persona de 6 ½ pies de altura proyecta una sombra de 4 pies. Al mismo tiempo, un poste proyecta una sombra de  25 pies. ¿Qué altura, en pies, tiene el poste?

a) 40 5/8 

b) 42

c) 40 ¼

d) 45

e) 40 ½ 

18. Una casa y un terreno cuestan $150,000.00. Si la casa cuesta el doble que el terreno, ¿cuánto cuesta la casa?

a) $50,000

b) $100,000

c) $75,000

d) $40,000

e) $110,000

19. El área de un circulo es 28 centimetros cuadrados , calcule la medida aproximada del radio.

a) 9 cm

b) 8 cm

c) 4 cm

d) 3 cm

e) 5 cm

20. ¿Cuál expresión muestra el volumen de la siguiente figura si de largo mide “y” y un lado de su base cuadrangular es de 6? 

21. Obtén el perímetro de la siguiente figura.

22. Si en un juego de foot ball el equipo anfitrión obtuvo el triple de puntaje que el equipo visitante, cual expresión muestra  el puntaje del equipo visitante si el puntaje de ambos equipos fue de 132?

23. Calcula el área de la siguiente figura.

24. Representa la siguiente cantidad en notación científica   .000048

25. Juan y Marcos viajaron en línea recta, mientras Juan se dirigió hacia el norte 25 millas mientras Marcos manejo 32 millas hacia el este. Una vez que se detienen, ¿aproximadamente, qué distancia los separa a ambos?

a) 45 millas

b) 40 millas

c) 38 millas

d) 50 millas

e) 57 millas

26. Adela organizo la fiesta de cumpleaños de su hija. Si  acudieron 18 adultos y 20 niños, ¿cuál es la razón de niños a adultos?

1. 18 y 20
2. 4 a 5
3. 9:10
4. 10 a 9
5. 8:10

27. Un rectángulo mide 3x de ancho y 8x de largo. ¿Cuál es el área del rectángulo?

28. En un triangulo rectángulo un ángulo mide 10˚ mas  que el más chico. ¿Cuál expresión expresa la medida del ángulo más chico?

1. (10 + x) + 90 = 180
2. x + 2x + 90 = 180
3. x + (x – 10) + 90 = 180
4. x (x + 10) + 90 = 180
5. (x + 10) + x + 90 = 180

29. La arista de un cubo mide 4x. ¿Cuál es el volumen del cubo?

30. Un tráiler va a ser cargado con 10 cajas cuadradas de 5 pies cada una. Si las dimensiones del tráiler son de 40 pies de largo y 8 de ancho y 10 de altura. ¿Cuánto espacio libre queda en el tráiler?

31. Si el área de un rectángulo es de 18 y su base es el doble que lo ancho. ¿Cuánto mide cada uno respectivamente?

1. 2 y 4
2. 3 y 9
3. 2 y 6
4. 3 y 6
5. 4 y 8

Extensión de litorales (km)

FUENTE: INEGI. México en el Mundo. 

32. ¿Cuál es la diferencia de litorales entre México y  Perú?

33. ¿Cuál es la mediana de la extensión litoral de estos países?

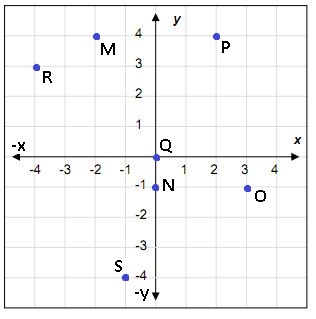
34. ¿Qué distancia hay entre el punto M y O?

35. Encuentra el valor de la siguiente expresión 

36. Si el área de un círculo es de 200.96. ¿Cuál expresión permitiría encontrar el radio?

37. ¿Cuál es la moda de los gastos que son considerados muy caros?

38. ¿Cuál es el promedio de número de personas que consideran que los bienes y servicio servicios son muy caros?

39. ¿Cuál es la razón de las personas que consideran que el gasto en alimentos es muy caro con las que consideran que es justo?

40. Obtén la mediana de las personas que consideran que los bienes y servicios son justos.

41. Una carnicería necesita surtir un pedido  de 15  ¼  de libras de carne, y solo cuenta con 1/3 de esa cantidad. ¿Cuánta carne le hace falta  completar el pedido?

42. Martha va a cocinar una olla de pozole cuyas dimensiones son 50 cm de altura y tiene un radio de 3 cm. Si solo llena ½ de olla con agua. ¿Qué espacio queda vacio?

43. Armando tiene dos trabajos de medio tiempo. Por las mañanas  cubre un horario de 8:30 a 12:15p.m y por las tardes de 5:00 a 9:30 pm.  (Descansa sábados y domingos). ¿Cuántas horas trabajo en las últimas dos semanas?

44. Si le pagan a 13 dólares la hora, ¿cual expresión muestra cuanto gano en esas dos semana?

1. (4 ¼ x 4 ½) + 13 x 2
2. 12 + 4 ¼ + 4 ½ x 2
3. 8 ¼ + 13 +2  x 5
4. (3 ¾ + 4 ½) x 2 x 5 x 13
5. (4 ¼ + 4 ½) ÷ 13 x 2

45. Resuelva

46. La matricula escolar de una escuela a inicio del año es de 246 estudiantes, si al final del año solo se gradúan 2/3 de esa cantidad. ¿Cuántos estudiantes desertaron en total?

47. Carla camina  ¼ de milla para llegar a su trabajo. ¿Cuánto camina, de ida y vuelta, durante la semana si trabaja 5 días a la semana?

48. ¿Qué porcentaje de personas optan por visitar a un medico en farmacias?

49. ¿Cuál es la razón de las personas que cambian a un medicamento genérico intercambiable con aquellos que optan por conservar su medicamento original?

50. ¿Cuántas más personas deciden asistir a consulta al sector publico con aquellas que deciden acudir al sector privado?

RESPUESTAS

 

Aritmética

ARITMETICA es una de las ramas mas antiguas de las matemáticas  en la que se aplican las operaciones básicas como suma, resta, multiplicación, división, potencia y raíz cuadrada. Para el examen del GED es indispensable el dominio de estas operaciones ya que son fundamentales para la solución de problemas verbales y de razonamiento.

Fracciones

Las FRACCIONES expresan una parte de un todo o un entero que puede ser cualquier numero natural u objeto o cosa que pueda ser divido. También se conocen como quebrados.

Geometria

La GEOMETRIA, una de las ramas mas antiguas de las matemáticas se encarga de estudiar las propiedades de las figuras geométricas; no solo abarca las áreas, volúmenes y longitudes, su campo de aplicación práctica en la arquitectura, astronomía, topografía, mecánica, etc.

Algebra

La ALGEBRA como una de las principales ramas de las matemáticas en la que se usa un lenguaje diferente al de aritmética, una de las principales diferencias es que los números se representan con símbolos que usualmente son letras del alfabeto.

Recursos

En este espacio encontraras enlaces que faciliten el estudio de las matemáticas.