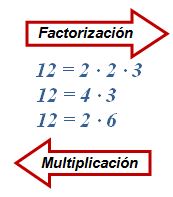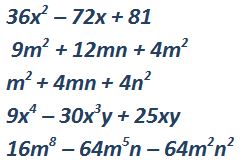
Factorización de trinomios cuadrados perfectos
De la factorización de trinomios, el de cuadrados perfectos es uno de los más fáciles ya que solo tenemos que entender el concepto de la raíz cuadrada perfecta, que no es otra cosa que buscar el número que multiplicado por el mismo nos de el valor que buscamos, por ejemplo la raíz cuadrada de 25 es 5 porque 5 por 5 es 25 y así sucesivamente, este tema lo puedes revisar el siguiente video.
Al buscar los factores de un trinomio cuadrado perfecto se van a obtener aquellos que multiplicados por sí mismo nos dan el trinomio. Si ya sabes multiplicar factores se te va a facilitar entender este tema, veamos el primer ejemplo y los pasos para resolverlo:
Antes de aplicar este método de factorización debes determinar si el primer y tercer término del trinomio son cuadrados perfectos, en el caso de las incógnitas o letras, solo es ver si su exponente es par, quiere decir que la raíz cuadrada de x4 = x2, de m6n2 = m3n y así sucesivamente.
x2 + 6x + 9
PASO I
Obtener la raíz del primer término (azúl), abrir un paréntesis y poner la respuesta. (Para obtener la raíz cuadrada de cualquier incognita, simplemente se divide el exponente entre 2).
(x
PASO II
Identificar el signo de segundo término (verde) y escribirlo enseguida.
(x +
PASO III
Obtener la raíz cuadrada del tercer término (rojo), escribelo después del signo y cerrar el paréntesis.
(x + 3)
PASO IV
Elevar al cuadrado la respuesta.
(x + 3)2
Ejemplo II
x4 + 4x2y + 4y2
PASO I
Obtener la raíz cuadrada del primero y tercer término – azul y rojo- (recuerda que los exponentes de las incógnitas se dividen entre dos).
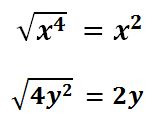
PASO II
Escribir las respuestas dentro de un paréntesis.
(x2 2y)
PASO III
Escribir el signo del segundo término y elevas al cuadrado.
(x2 + 2y)2
Para comprobar la respuesta, simplemente se multiplica el binomio por el mismo.
(x2 + 2y) (x2 + 2y)
x4 + 4x2y + 4y2
Ejercicios de practica
- 4 – 4x + x2
- 4x2 + 12x + 9
- x2y2 + 8xy +16
- 25m2 – 10mn + n2
- m2n2 + 10mn + 25
- 36x2 – 108x + 81
- 9m2 + 12mn + 4n2
- m2 + 4mn + 4n2
- 9x4 – 30x3y + 25x2y2
- 16m8 – 64m5n – 64m2n2
RESPUESTAS
Las respuestas las puedes representar (x – 2)2 o (x – 2) (x – 2)
- (x – 2)2
- (2x + 3)2
- (xy + 4)2
- (5m – n)2
- (mn + 5)2
- (6x – 9)2
- (3m + 2n)2
- (m + 2n)2
- (3x2 – 5xy)2
- (4m4 – 8mn)2
Pasos para resolverlos
1. x2– 4x + 4 Primero verifica que el trinomio este ordenado
- (x ) (x ) Obten la raíz del primer término – separando las x
- (x 2) (x 2) Obten la raíz del tercer término – √4 = 2
- (x – 2) (x 2) En el primer factor escribes el signo del segundo término.
- (x – 2) (x – 2) Multiplicas el singo del primer término por el signo del tercero. – por + = –
2. 4x2 + 12x + 9
- (2x ) (2x ) Obten la raíz del primer término – √4 = 2 y √x2 = x
- (2x 3) (2x 3) Obten la raíz del tercer término – √9 = 3
- (2x + 3) (2x 3) En el primer factor escribes el signo del segundo término.
- (2x + 3) (2x + 3) Multiplicas el singo del primer término por el signo del tercero. + por + = +
3. x2y2 + 8xy +16
- (xy ) (xy ) Obten la raíz del primer término – √x2 = x y √y2 = y
- (xy 4) (xy 4) Obten la raíz del tercer término – √16 = 4
- (xy + 4) (xy 4) En el primer factor escribes el signo del segundo término.
- (xy + 4) (xy + 4) Multiplicas el singo del primer término por el signo del tercero. + por + = +
4. 25m2 – 10mn + n2
- (5m ) (5m ) Obten la raíz del primer término – √25 = 5 y √m2 = m
- (5m n) (5m n) Obten la raíz del tercer término – √n2 = n
- (5m – n) (5m n) En el primer factor escribes el signo del segundo término.
- (5m – n) (5m – n) Multiplicas el singo del primer término por el signo del tercero. – por + = –
5. m2n2 + 10mn + 25
- (mn ) (mn ) Obten la raíz del primer término – √m2 = m y √n2 = n
- (mn 5) (mn 5) Obten la raíz del tercer término – √25 = 5
- (mn + 5) (mn 5) En el primer factor escribes el signo del segundo término.
- (mn + 5) (mn + 5) Multiplicas el singo del primer término por el signo del tercero. + por + = +
6. 36x2 – 108x + 81
- (6x ) (6x ) Obten la raíz del primer término – √36 = 6 y √x2 = x
- (6x 9) (6x 9) Obten la raíz del tercer término – √81 = 9
- (6x – 9) (6x 9) En el primer factor escribes el signo del segundo término.
- (6x – 9) (6x – 9) Multiplicas el singo del primer término por el signo del tercero. – por + = –
7. 9m2 + 12mn + 4n2
- (3m ) (3m ) Obten la raíz del primer término – √9 = 3 y √m2 = m
- (3m 2n) (3m 2n) Obten la raíz del tercer término – √4 = 2 y √n2 = n
- (3m + 2n) (3m 2n) En el primer factor escribes el signo del segundo término.
- (3m + 2n) (3m + 2n) Multiplicas el singo del primer término por el signo del tercero. + por + = +
8. m2 + 4mn + 4n2
- (m ) (m ) Obten la raíz del primer término – √m2 = m
- (m 2n) (m 2n) Obten la raíz del tercer término – √4 = 2 y √n2 = n
- (m + 2n) (m 2n) En el primer factor escribes el signo del segundo término.
- (m + 2n) (m + 2n) Multiplicas el singo del primer término por el signo del tercero. + por + = +
9. 9x4 – 30x3y + 25x2y2
- (3x2 ) (3x2 ) Obten la raíz del primer término – √9 = 3 y √x4 = x2
- (3x2 5xy) (3x2 5xy) Obten la raíz del tercer término – √25 = 5 , √x2 = x y √y2 = y
- (3x2 – 5xy) (3x2 5xy) En el primer factor escribes el signo del segundo término.
- (3x2 – 5xy) (3x2 – 5xy) Multiplicas el singo del primer término por el signo del tercero. – por + = –
10. 16m8 – 64m5n – 64m2n2
- (4m4 ) (4m4 ) Obten la raíz del primer término – √16 = 4 y √m8 = m4
- (4m4 8mn) (4m4 8mn) Obten la raíz del tercer término – √64 = 8, √m2 = m y √n2 = n
- (4m4 – 8mn) (4m4 8mn) En el primer factor escribes el signo del segundo término.
- (4m4 – 8mn) (4m4 – 8mn) Multiplicas el singo del primer término por el signo del tercero. – por – = –