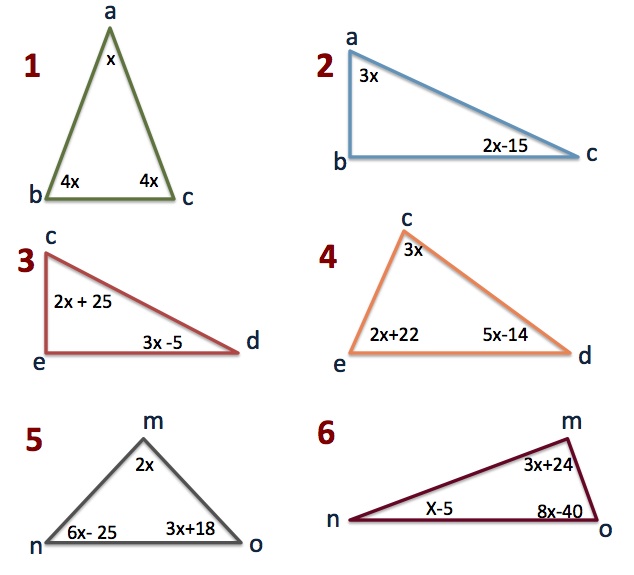
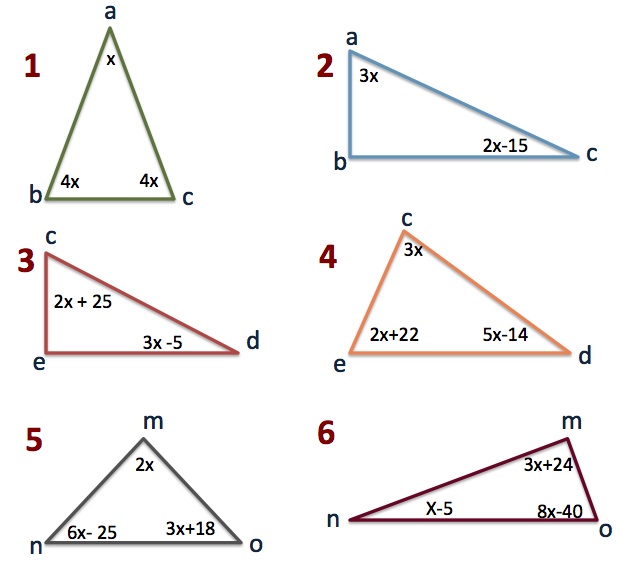
Otra aplicación del Álgebra continua en los ángulos dentro de un triángulo, después de todo el trabajo de matemáticos y otros genios que nos antecedieron, sabemos que la medida de los ángulos internos de cualquier triángulo va a ser siempre de 180°, sin importar el tipo de triangulo que sea.Para poder resolver estos ejercicios es indispensable entender los siguientes temas: suma de números con signo, multiplicación de # con signo, suma de términos. 1. x + 4x + 4x = 180 (suman los términos semejantes) 9x = 180 (se pasa el 9 al otro lado del signo igual, si esta multiplicando se pasa dividiendo) x = 180/9 (se divide 180 entre 9) x = 20 (para obtener el valor de cada ángulo, se multiplica 4 por el valor de “x” = 20, por tanto 4(20) = 80 grados.En el ejemplo 2 hay un ángulo recto que siempre mide 90°, quien este familiarizado con las ecuaciones va a encontrar mas fácil plantearla así 3x + 2x – 15 = 90. Tomando en cuenta solo las medidas del angulo «a» y «c».2. 3x + 2x – 15 + 90 = 180 (simplificar términos y números) 5x + 75 = 180 (el 75 esta sumando se pasa del otro lado del signo igual restando) 5x = 180 – 75 (el 5 esta multiplicando, pasa al otro lado del signo igual dividiendo) x = 105/5 (se divide 105 entre 5) x = 21 El ángulo “a” se obtiene multiplicando 3 por el valor de “x” 3(21) = 63El valor del ángulo “c” se obtiene multiplicando 2 por el valor de “x” y restando 15; 2(21)-15 = 27El ángulo “b” es recto y siempre mide 90 grados.Revisa el siguiente video y posteriormente resuelve los siguientes ejercicios, las respuestas las encuentras al final. Preguntas, dudas o comentarios los puedes compartir al final del articulo.
EJERCICIOS DE PRACTICA

Help please
todas me salieron mal, simplemente no entiendo, en el 2 que no se supone que b tiene que ser 90???????
please help me
Hola , me gustaria entender una ecuacion que la entiendo mucho, es : 6×-25+2×+3×+18 =180
Hola Sandro, aquí está el tema de ecuaciones para que tengas practica extra.
Para está ecuación estos son los pasos.
6×-25+2×+3×+18 =180 -Primero sumas o restas los términos semejantes
11x – 7 = 180 Despejas el -7 con signo positivo
11x = 180 + 7 sumas y despejas el 11 dividiendo
x = 187/11
x = 17
esa es muy facil, a mi me ponen asi y7+O8=180-x2
en la tuya x=188
Espero quede claro 😀
Si en la 2 la «b» es 90 grados, al plantear la ecuacion puedes poner 3x +2x -15 = 90 (no incluimos b, ya sabemos que mide 90), despues sumas las x =5x, sumas 90 +15 = 105 (5x=90+15), finalmente divides 105 entre 5 = 21. El valor de x es 21. El angulo a es tres veces x osea 3 por 21= 63 y el angulo «c» es 2 veces x menos 15, que seria 2 por 21=42 – 15 = 27.
Espero se aclare tu duda 😀
(2m + 10°) + (3m)
(2m + 10°) + (3m) Elimina paréntesis multiplicando signos
2m + 10° + 3m Suma o resta términos semejantes
5m + 10°
???
Hola Luz, No entiendo esto.. Si puede resolver la #4 porfavor. Gracias
Porque es un ángulo recto
Porque mide 90°, dependiendo la medida, cada ángulo tiene un nombre. El llano mide 180°, el agudo mide menos de 90° y mas de 0°, el bostuso es mayor de 90° y menor que 180°
No pude resolver el triángulo #3 necesito ayuda gracias
La ecuación queda asi:
2x+25+3x-5+90=180 Simplificas términos semejantes, el 90 es del ángulo recto.
5x + 110 = 180 Despejas el 110 con signo negativo
5x = 180-110
5x = 70 Despejas el 5 dividiendo
x = 70/5
x = 14
Sustituyes el valor de «x» para obtener el valor de los ángulos
pero si uno ya sustituyo eso que 53 mas 90 es 37 queda la respuesta que hago si esta x = 14 despues de eso ayudame please
Solo sustituyes el valor de «x» para cada ángulo: 2x + 25, quitas la «x» y pones el 14. Queda:
2(14) + 25 mutiplicas
28 + 25 sumas
53
El otro es 3x – 5, sustituyes el valor de «x»
3(14) – 5 multiplicas 3 por 14
42 – 5 restas
37
El valor del ángulo recto siempre es 90
Me pueden ayudar con la solución del Triángulo número 3 gracias
La ecuación queda asi:
2x+25+3x-5+90=180 Simplificas términos semejantes, el 90 es del ángulo recto.
5x + 110 = 180 Despejas el 110 con signo negativo
5x = 180-110
5x = 70 Despejas el 5 dividiendo
x = 70/5
x = 14
Sustituyes el valor de «x» para obtener el valor de los ángulos
#4
Esta es un poco mas dificil ya que requiere mas pasos, primero planteas la ecuacion (la suma de todos los angulos es igual a 180) 3x+2x+22+5x-14=180. Sumas las «x» y simplificas los numeros -puedes revisar este enlace si no sabes como hacerlo https://www.spanishged365.com/lun-07112011-1037/0peracion-de-numeros-con-signos en este caso restarias 22-14=8
Entonces tendrias 10x+8=180 (el 8 esta sumando de lado izquierdo, hay que despejarlo al lado derecho restando)
10x= 180-8 (finalmente el 10 esta multiplicando a la «x», pasaria dividiendo)
x = 172/10 entonces el valor de la x= 17.2
Angulo c= 3x = 3(17.2) = 51.6
Angulo e= 2x+22 = 2(17.2) +22= 56.4
angulo d = 5x-14 = 5(17.2) – 14 = 72
Thank you!
Gracias Luz por su ayuda, ahora ya entendí la operacion,
Si es + pasa – restando y si es – pasa + sumando, y el numerador
pasa ÷ dividiendo. Corríjame porfavor.
Le cuento que resolví los 6 ejersicios y estoy Felíz porque si pude
resolverlos gracias a su explication, ???? solo que la #3
el valor de "x" es 16, //// C 2(16) +25 = 57 /// E 3(16) -15 =33
D =90
Valor de «x»
En la 3 el valor de «x» es 14. Como es un triangulo rectángulo puedes desde un inicio simplificar la ecuación y te quedaría 2x+25+3x-5=90 porque eliminamos los 90 del ángulo recto, si los incluyes tendrías 2x+25+3x-5+90=180 -pero se requiere más pasos-
Usando la primera ecuación sumas las «x» y restas o sumas los números, te quedaría 5x+20=90, despejas el 20 restando 5x=90-20 y por último, despejas el 5 dividiendo x= 70/5 y te da x=14. Sustituyes valores y te da la medida de los ángulos.
Hola luz me dió 53 hice lo que me lo que dijo porque no me sale
Hola Santiago, si te refieres al ejercicio 3, estos son los pasos.
90+2x+25+3x-25 = 180 sumas y restas términos semejantes del lado izquierdo
110 + 5x = 180 despejas el 110, esta positivo pasa negativo a la derecha.
5x = 180 – 110 despejas el 5 esta multiplicando, paso dividiendo al 70
x = 70 entre 5
x = 14 el valor de x es 14
Como el ángulo c es 2x + 25, sustituyes el valor de «x» y sumas 25. 2(14)+25 = 53
necesito su ayuda no entiendo estos ejercicios de practica
Pasos/ecuaciones
Los puedes resolver planteando una ecuacion pero hay que tener presente que los angulos internos de los triangulos siempre suman 180 grados. (los angulos son las partes internas del triangulos. Por ejemplo en el ejercicio uno debes sumar todas las «x» y son 9x, planteando la ecuacion podria ser 9x = 180, ( o tambien x+4x+4x = 180) para obtener el valor de la «x» debes despejarla, la regla es que si el nueve esta multiplicando a la «x» hay que despejarlo del otro lado del signo igual dividiendo, entonces x = 180/9 (dividir 180 entre 9) el valor de la x = 20. El valor de los angulos «b» y «c» se obtiene de multiplicar 4 por el valor de la x = 4 (20) y el resultado es 80 grados cada uno. Es importante entender lo basico de algebra para poder entender las ecuaciones, si ya entiendes bien los temas de suma, resta, multiplicacion y division de numeros con signos, sigue con suma y multiplicacion de terminos y simplificacion de terminos. No tengo un video sobre ecuaciones, espero pronto poder bajar uno para explicar mas estos temas. Ya inclui los pasos para resolver los primeros dos ejercicios, espero quede mas claro.
Ruiz cuadrada
Hola maestra, necesito aprender bien como sacar la raiz cuadrada, me puede ayudar por favor?.
Video-raiz cuadrada
Hola Julieta, todabia no tengo un articulo sobre la raiz cuadrada, pero hay un video, considera revisarlo; solo ten presente que para la raiz cuadrada no se evalua el procedimiento para obtenerla, lo importante es tener nocion general de lo que representa. Revisa el video y si tienes dudas me avisas. http://youtu.be/LHUwC-Sz1WQ
Raiz cuadrada
Gracias por darse el tiempo de responder maestra. Ya mire el video, lo que me pasa esque no e podido resolver la raiz de 58, en uno de los ejercicios para resolver la distancia entre los puntos de el plano cartesiano (RS) mi respuesta me da 7.3 y la respuesta en la calculadora me da 7.6.
Lo reviso
Si es 7.6. Ahora, este en es el caso, pero hay preguntas donde te piden la raiz cuadrada y si te diecen «aproximada» no va a ser exacta. Una manera sencilla de provar que es 7.6, usando las raices cuadradas exactas; si 7×7=49 y 8×8=64, el 58 esta aproximadamente a la mitad por lo que la raiz cuadrada debe ser aproximadamente la mitad entre 7 y 8 osea que debe ser mayor de 7.5. Espero te quede mas o menos claro porque es un poco complicado explicarlo aqui. Saludos!
Gracias
Nuevamente gracias maestra, me quedo clara su explicacion ahora solo me toca practicar un poco. Saluditos…!
ayuda
biendo loscomentarios anteriores pude vermi error en la ecuacion #3
ahora que se que devo de dejar a un lado el 90 porque es una de las
respuestas que busco me podria poner los pasos a seguir si incluyo
el noventa en la ecuacion.
porque de primero lo ponia y nadamas no me salia bien mi respuesta.
de antemano muchas gracias
Ecuación
La acomodarías así: 90 + 2x + 25 + 3x -5 = 180, sumas y restas las «x» y los números, te da 5x + 110 = 180, despejas el 110 restando porque esta sumando, 5x = 180 -110 y por último el cinco está multiplicando, lo despejas dividiendo x = 70/5 y el valor de x=14.
ayuda
en un ejemplo del video si agregas 90 grados pero en el ejemplo ejercicio numeo 2 dices que no se agrega por que ya sabemos que b es igual a 90 grados pero por que en el ejercico del video si lo agregastes y tambien sabiamos que la b eran 90 grados ?? eso me confunde por que como vamos a saber cuando o cuando no lo agregamos a la simplificasion???
tambien en el ejercicio
tambien en el ejercicio numero dos por que es =90 se supone que deveria ser =180 no entiendo ayuda…
Mismo resultado con diferente ecuación.
3x + 2x -15 + 90 = 180
3x + 2x – 15 = 90
Ambas ecuaciones te van a dar el mismo resultado, en la primera estas sumando los tres angulos y la suma de los angulos internos de un triangulo siempre es 180. Por tanto si a=3x; b= 90; c= 2x-15 (el ángulo «b» es una angulo recto y siempre mide 90 grados). Al sumar estos tres angulos te queda esta ecuación: 3x + 2x -15 + 90 = 180
El segundo método es considerar solo los angulos «a» y «c» porque la suma de esos dos es 90, aquí no estas considerando el ángulo «b», entonces sumas a=3x mas c=2x-15 y queda esta ecuación: 3x + 2x – 15 = 90
Espero quede claro :), saludos!!
ejercicio # 6
Por favor quisiera ver paso a paso el ejercicio # 6, qu mis resultados son distinto; angulo n = 8.25, angulo m = 63.75, y el angulo o = 66, la X = 13. 25,gracias….
Pasos
x-5+3x+24+8x-40 =180 sumas términos semejantes
12x -21 =180 Despejas el 21- cambia el signo-
12x=180 +21 Sumas
12x=201 Despejas el 12, esta multiplic. pasa divid.
x=201 ÷ 12 divides
x= 16.75
n = x-5 / 16.75 – 5= 11.75
m = 3x + 24 / 3(16.75) + 24 = 74.25
o = 8x- 40 / 8 (16.75) – 40 = 94
Ayuda con algebra y triangulos
Gracias por su tiempo y amabilidad. no se como resolberlos ya mire el video y sigo sin entender si por fabor me pudiera ayudar.
Ecuaciones
¿Cómo estan en ecuaciones? te recomiendo que revises este enlace y probablemente te facilite entender el tema. ECUACIONES
ESTOY MEJORANDO
TODAS ME SALIERON BIEN, CREO QUE ESTOY MEJORANDO 🙂 GRACIAS A SUS EJERCICIOS Y EXPLICACIONES 🙂 QUE TENGA UN BUEN DIA.
Buen trabajo!!!
Me alegra, recuerda que la práctica hace al maestro!!!! Un saludo!
hola maestra
el ejercicio 5 me sale m 31.4, n 69.1, o 65.1 x=15.72 por que dividi 173 entre 11 , hago mas?
Ejercicio 5
No es 173, debe darte 187 por eso tu resultado es diferente.
A mí también me dió 173 lo podría explicar
Hola Natalia, ¿a cuál ejercicio te refieres? ¿podrías indicarme Saludos!
triangulos
Puedes usar http://triancal.esy.es (calculadora de triángulos online) para dibujar y calcular cualquier triángulo.
==>Google Chrome
You can use http://triancal.esy.es (online triangle calculator) to calculate and draw any triangle.
Gracias por la información Jesus
Gracias voy a poner aquí el enlace para que los lleve directo Dibujar triangulos en linea
con urgencia
Buen dia necesitaria con urgensi si es posible resuelto estos ejercicios ya que no recuerdo como se hacen y mi hijo no entiende
1)encontrar el valor de X y luego descubrir el valor de los angulos sabiendo que la suma de los angulos interiores es 180
A= 2X-15
B= X-26
C= 39
2) si la suma de los lados del borde de la pileta es igual a 180mts (A+B+C+D+E+F=184M) ¿CUANTO MIDE CADA LADO?
A= X+2
B=X
C= X
D= X+2
E= X
F= X
DESDE YA MUCHAS GRACIAS SALUDOS CORDIALES
no me dio el resultado del 5 podrian ayudarme?
La ecuación queda así: 2x+6x-25+3x+18=180 Primero suma todas las «x»
11x-25+18=180 ahora resta los números
11x-7=180 pasas el -7 a la derecha con signo positivo
11x = 180+7 sumas y pasas el 11 a la derecha dividiendo
x = 187/7
x = 17
ángulo
m= 2(17) = 14
n = 6(17)-25 = 77
d = 3(17)+18 =69
Me pueden ayudar con esto él triangulo esta partido a la mitad en una esquina alfa y arriba 37 grados en la otra mitad arriba beta y abajo 60
me pueden dar las operaciones y resultado de la 3,4,5y6
Te dejo los pasos del ejercicio seis, para los demás sigues los mismos pasos.
x-5+3x+24+8x-40 = 180 Identifica términos semejantes y suma o resta según corresponda.
12x – 45 + 24 = 180 Resta números con signos diferentes y deja el signo del número mayor.
12x – 21 = 180 Despeja el – 21, es negativo, pasa positivo a la derecha.
12x = 180 + 21 Sumas
X = (180 + 21) ÷ 12 El doce pasa dividiendo a la derecha porque está multiplicando a la «x»
X =16.75
N → 16.75 – 5 = 11.75
O → 8(16.75) – 40 =
M → 3(16.75) + 24 =
Buenas tardes el ejercicio numero 4, 5 y 6 son triangulos interiores y exteriores?
Así es Juanita, deben sumar en total 180 grados.
Hola Luz, No entiendo el problema 6 Si puede resolverla porfavor. Gracias
x-5+3x+24+8x-40 = 180 Primero sumas términos semejantes
12x – 45 + 24 = 180 Restas y sumas
12x – 21 = 180 Pasas el -21 con signo positivo a la derecha
12x = 180 + 21 sumas y por último divides entre 12, porque el doce está multiplicando a la «x» y pasa dividiendo al otro lado del signo igual.
X = (180 + 21) ÷ 12
X =16.75 valor de x
N → 16.75 – 5 = 11.75
O → 8(16.75) – 40 = 94
M → 3(16.75) + 24 = 74.25
como hago la recta de (7)+(-14)=
Juan, este ejercicio no es para graficarse. Se resuelve multiplicando signos y sumando y restando.
(7) + (-14) multiplicas signos + por – = –
7 – 7 restas y te da cero.
Las ecuaciones que se grafican son las de formato y = mx + b, la m representa la pendiente y la b el intercepto en «y».
me podrían por favor explicar la 4
3x+2x+22+5x-14=180 Suma y resta los términos semejantes
10x + 8 = 180 Despejas el ocho restando
10x = 180 – 8 restas el 8 y despejas el 10 multiplicando
x = 172/10
x = 17.2
Para obtener el valor de los ángulos sustituye el valor de «x»
c = 3(17.2) =51.6
e = 2(17.2) + 22 = 56.4
d = 5(17.2) – 14 = 72
Cual el valor de x?
La «x» es una incógnita y su valor siempre varia dependiendo la ecuación. Para entender un poco más sobre el tema puedes revisar este tema: https://www.spanishged365.com/ecuaciones-de-un-solo-paso/
holA DONDE estan las respuestas de la
5
perdon me puede decir cual es la 5
Está en las respuestas, o a que te refieres o.O
m = 34; n = 77; d = 69
me puedes decir los pasos de el punto #5
2x + 6x -25 +3x +18 = 180 Sumas las «x» y los enteros por separado
11x – 7 = 180 Despejas el -7 sumando
11x = 180 + 7 despejas el 11 dividiendo
x = 187/11
x = 17
Para obtener los valores de los ángulos solo sustituye el valor de «x»
2x
2(17) = 34
6x – 25
6(17) -25
102-25=77
3x +18
3(17)+18
51+18=69
Ayuda!!,
Nombre de ángulos:v
D, E y F
Es un triángulo rectángulo, “E” es un ángulo recto, “D”=2x y “F”=3x-15
Ayudaaa es para hoy!
Me podrían ayudar con 2x+3x+x
Cuando tenemos términos semejantes (que tienen el mismo número, la misma letra y el mismo exponente) solo se suman o restan. Como todos son positivos, solo hay que sumar.
2x+3x+x nos da 6x. La «x» sola equivale a 1 es como si tuvieras 2x+3x+1x
Gracias por los ejercicios, a mi pequeño le sirvió para comprender mas las ecuaciones le fue un poco complicado pero no difícil, si pudiera poner otros ejercicio se lo agradecería
Gracias por tu comentario Ariel, me alegra saber que los ejercicios le fueron de ayuda a tu hijo.
En estos enlaces hay algunos ejercicios de ecuaciones. Saludos 🙂
https://www.spanishged365.com/algebra-angulos-y-ecuaciones/
ECUACIONES DE PRIMER GRADO
VIDEO: https://youtu.be/LKZ5BgWsEtc
EJERCICIOS:
http://www.spanishged365.com/223/ecuaciones
hola no se como hacer la 3 y la 4
La #3
La ecuación queda asi:
2x+25+3x-5+90=180 Simplificas términos semejantes, el 90 es del ángulo recto.
5x + 110 = 180 Despejas el 110 con signo negativo
5x = 180-110
5x = 70 Despejas el 5 dividiendo
x = 70/5
x = 14
Sustituyes el valor de «x» para obtener el valor de los ángulos
#4
Esta es un poco mas dificil ya que requiere mas pasos, primero planteas la ecuacion (la suma de todos los angulos es igual a 180) 3x+2x+22+5x-14=180. Sumas las «x» y simplificas los numeros -puedes revisar este enlace si no sabes como hacerlo https://www.spanishged365.com/lun-07112011-1037/0peracion-de-numeros-con-signos en este caso restarias 22-14=8
Entonces tendrias 10x+8=180 (el 8 esta sumando de lado izquierdo, hay que despejarlo al lado derecho restando)
10x= 180-8 (finalmente el 10 esta multiplicando a la «x», pasaria dividiendo)
x = 172/10 entonces el valor de la x= 17.2
ángulo c= 3x = 3(17.2) = 51.6
ángulo e= 2x+22 = 2(17.2) +22= 56.4
ángulo d = 5x-14 = 5(17.2) – 14 = 72
Valor de los ángulos π y B
A
a^=70° 15′
e^ = 50° 45′