Cuando nos presentan una ecuación lineal de la forma y = mx + b, sabemos que podemos obtener los valores de las variables (x, y) y representar la función (recta) en el plano cartesiano, en el siguiente tema vamos a trabajar con dos ecuaciones juntas y lo primero es que vamos a buscar el punto donde se cruzan estas rectas aplicando el método de eliminación por sustituían.
Si el tema se te dificulta, considera revisar los temas previos:
- Plano cartesiano
- Pendiente
- Métodos para obtener la pendiente
- Graficar una ecuación
- Ecuación de una recta
Ahora iniciemos con un ejemplo sencillo
Si tenemos:
x + y = 6
x – y = 4
En estas dos ecuaciones los valores de “x” y “y” van a ser los mismo pero el resultado va a ser diferente, en la primera debemos buscar dos números que sumados nos den 6 (primera) y esos mismos numero restados nos dé 4 (segunda). El único par que cumple esta función son el 5 y 1.
5 + 1 = 6
5 – 1 = 4
Este ejemplo es sencillo, pero si tenemos números más grandes que incluyan multiplicación se puede complicar un poco más así que veamos el método para resolverlas paso a paso.
EJEMPLO I
x + y = 9
10x + 5y = 60
En este ejemplo, hay que buscar un número (x) que sumado a otro número (y) nos de 9, esos mismos valores de “x” y “y” deben resolver la segunda ecuación donde se multiplica diez por el primer número (x) y se suma la multiplicación de cinco por el otro número (y) donde nos da como resultado 60.
PASO I
Hay que escoger un coeficiente (número) para igualarlos, si escogemos las “y” ambas ecuaciones deben tener 5y y si escogemos las “x” ambas deben tener 10x. Para este ejemplo vamos a igualar las “y” para tener en ambas ecuaciones 5x. Una debe ser negativa y la otra positiva.
PASO II
Ya que se elegieron cual coeficiente (número) que se van a igualar, se busca el mcm, que en este caso es el 5. Posteriormente se multiplica cada uno de los términos de la primera ecuación por -5. (El cinco debe ser negativo porque queremos que en la primera ecuación nos de -5y.
– 5 ( x) = – 5x
– 5 (y) = – 5y– 5 (9) = – 45Y la ecuación quedaría así: – 5x = 5y = – 45
PASO III
Una vez que se multiplica la ecuación, se acomoda en orden para sumar o restar ambas ecuaciones
-5x – 5y = – 45
10x + 5y = 60
5x / = 15
x = 3
PASO IV
Ya restada la ecuación, solo queda despejar y obtener el valor de “y” en cualquiera de las dos ecuaciones.
10x + 5y = 60 Sustituimos el valor que obtuvimos de «x» en la ecuación.
10(3) +5y = 60 Se multiplica 10 por 3 y se despeja del otro lado de la ecuación.
30 + 5y = 60
5y = 60 – 30
y = 30/5
y = 6
Por tanto el punto de intercepción de ambas ecuaciones es (3, 6)
PASO V
Representa los valores de “x” y “y” en el plano cartesiano que indican donde se cruzan ambas rectas. (3, 6)
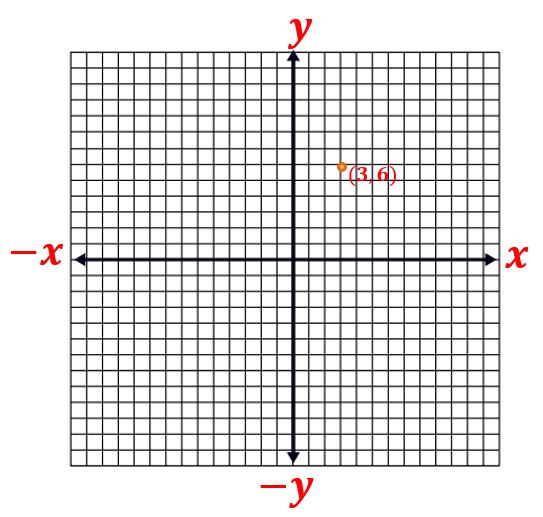
PASO VI
Obtener dos valores más de cada función y graficar para representar las rectas. Esto se hace asignando valores a la “x”, tu respuesta puede variar dependiendo que valores asignes, pero la recta debe tener la misma dirección. Si no sabes cómo graficar una ecuación, revisa este enlace.
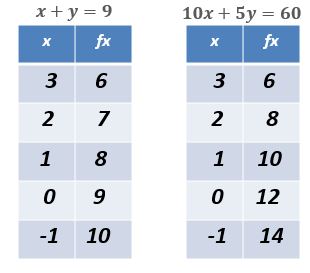
PASO VII
Graficar ambas funciones
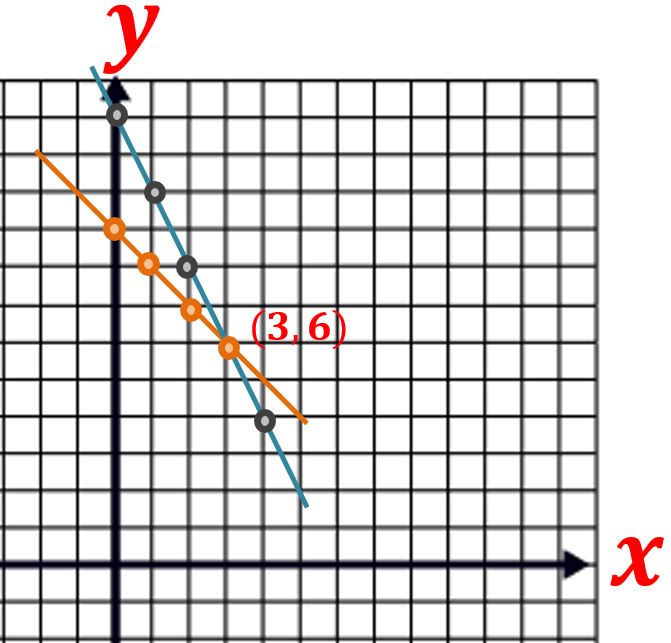
IMPORTANTE: Si se presenta el caso en el que los coeficientes (números) que queremos igualar tienen el mismo signo y no se puede restan, simplemente hay que cambiarle los signos a toda la ecuación.
Ejemplo II
2x + y = 7
x + 4y = 14
Siguiendo los pasos anteriores, igualamos la segunda ecuación para tener 2x multiplicando toda la ecuación por dos.
2 (x) = 2x
2 (4y) = 8y
2 (14) 28
Restando
2x + y = 7
2x + 8y = 28 (OJO, como puedes ver el 2x es positivo, hay que cambiarlo a negativo por tanto los signos de los términos restantes también cambian). Una vez cambiados, hay que restar.
2x + y = 7
– 2x – 8y = – 28
/ -7y = – 21
Despejas “y”
y = – 21 / – 7
y = 3
Una vez encontrado el valor de “y”, se siguen los pasos del IV al VII hasta que se grafiques ambas ecuaciones.
EJERCICIOS DE PRACTICA
- a) 3x + 2y = 8 b) 5x – y = 9
- a) 8x + 5y = 34 b) 4x – 2y = 8
- a) 2x – 6y = – 26 b) 15x + 3y = 93
- a) 9x – 15y = –39 b) 15x – 4y = –23
- a) 2x + 5y = 30 b) 6x + 4y = 46
- a) 3y + 5x = 4 b) 6y – 10x = –32
- a) 14y – 75x = – 38 b) –2y + 9x = 2
- a) 24x – 3y = –45 b) –12x + 5y =19
- a) 11y – 4x = 56 b) –15y + 2x = – 66
- a) 18x – 6y = 6 b) 27x – 24y = –117
- a) 6x – 2y = 26 b) 3x + 18y = –63

Diferentes resultados
wMaestra el primero y segundo ejercicio lo resultados son iguales a Los de usted pero en los otros ejercicios los resultados son diferentes y con decimal Por favor ayuda
Ejemplo II
Quizás uno de los errores es la aplicación de los pasos del ejemplo II, ninguno de los ejercicios debe dar decimal, mañana checo nuevamente cada ejercicio y te confirmo si hay algún error.
Matematicas
Matematicas
no entiendo!
en la numero dos se que x=3 y y=2 pero nose como llegar a ese resultado!
estas ecuaciones me parecen muy complicadas!
ecuaciones
Antes de estudiar este tema trata de dominar estos temas Graficar una ecuación, Ecuación de una recta
gracias 🙂
por fin entendi! ..pero me atore en la #4 cuando tengo numeros impares que debo hacer?
#4
En esta tienes que buscar el mcm y como ninguno de los números mas grandes es divisible entre los mas chicos hay que buscar uno mas grande que sea divisible entre ambos, tienes que ver con cual par de números es mas fácil trabajar y en ese caso las "x" son mas viables. Hay que multiplicar la primera ecuación por 5, 9x – 15y = -39 y la segunda ecuación por – 3 (ojo el tres es negativo porque uno de los términos debe ser negativo para restar) 15x – 4y = -23 pon mucha atención con con los signos de cada término al multiplicar) Después de multiplicar sigues los pasos de restar, despejar, etc.
gracias:)
muchas gracias por su ayuda
buen día maestra
Que tal maestra, le queria pedir de favor si podria poner ejemplos de como resolver expresiones racionales y ecuaciones se lo agradeceria mucho.
Gracias por la sugerencia Alis
Si hace falta ese tema y también algunos mas de factorización, espero pronto poder incorporar ejercicios de esos temas. Saludos!!!
estudiante Nuevo buscando dirreccion…
Soy Nueva aqui en esta pagina me gustaria estudiar para aser mi GED prueva en espanol. voy a tratar de afigurarme como empezar a estudiar por mi cuenta. Pero si ahy algien que me pudiera giar lo apreciaria mucho gracias…
Estudiar por cuenta propia
Hola, lo principal es identificar que materia quieres estudiar primero, se recomienda iniciar con la mas fácil, puedes ver los examenes de practica para determinar cual se te facilita mas. Una vez que te decidas, puedes rentar un libro en la biblioteca o comprarlo en amazon, también apoyarte con los contenidos que encuentres en nuestra pagina. Y si tienes oportunidad, busca un lugar donde ofrezcan clases cerca de tu domicilio incorporanto tu codigo postal en este enlace. Por último, si estudias algun tema aquí por lo general vas a encontrar comentarios sobre dudas o incluso dejar las tuyas. Saludos!!!
como encontrar una función sin una ecuación?
profe tengo un ejercicio en el que me dan una tabla de valores con numeros determinados y las dos ultimas casetas vacias. y ademas me dan numeros con los que debo llenar las casillas. numeros que deben ser parte de la funcion. pero no me dan ni una ecuacion ni una grafica. como logro resolver un ejercicio asi?
Función
Debes identificar si es una ecuación lineal (si los datos siguen una secuencia progresiva) por ejemplo si van de dos en dos, de cinco en cinco, etc., revisa los métodos para obtener la pendiente y al final se aborda lo de la función. En ese caso sería ecuación lineal. El otro tipo de función sería la que se hace con una parabola pero esa es más difícil de explicar. Otros temas que te pueden ayudar a entender ese tema : ecuaciones lineales,
Hola, buenas. Donde puedo encontrar un video de system de 2 eacuacione?
Se me hace mas facil para entender cuando veo el video.
Muchas gracia!
Hola Vero, no he publicado un video con ese tema, me hace falta también los de factorización. Espero pronto tenerlos listos. Saludos!
Buenas noches maestra he estado trabajando en estos ejercicios, pero la #10 se me ha dificultado resolverla creo que el detalle esta en los signos la verdad no encuentro la respuesta..
Hola Mayra, disculpa la demora, una ecuación está incorrecta en lugar de 21 debe ser 27 a) 18x – 6y = 6, b) 27x – 24y = –117
Muchas gracias por el comentario, si no ni me abría dado cuenta.